The Maximum CPR Model: a demographic tool for family planning policy

Kristin E Bietsch; Emily Sonneveldt

doi:10.12688/gatesopenres.13094.2

Home Browse The Maximum CPR Model: a demographic tool for family planning policy

ALL Metrics

Views

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

Revised

The Maximum CPR Model: a demographic tool for family planning policy

[version 2; peer review: 2 approved]

Kristin E Bietsch ¹, Emily Sonneveldt¹

PUBLISHED 19 Feb 2020

Author details Author details

¹ Avenir Health, Glastonbury, Connecticut, 06033, USA

Kristin E Bietsch
Roles: Conceptualization, Data Curation, Formal Analysis, Methodology, Software, Writing – Original Draft Preparation

Emily Sonneveldt
Roles: Conceptualization, Funding Acquisition, Methodology, Project Administration, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS

Abstract

The Maximum CPR Model (MCM) allows demographers, policy makers, and family planning advocates to determine a country’s highest potential contraceptive prevalence rate (CPR), based on an ideal number of children, demographic life events, and population structure. Understanding the highest potential level of CPR achievable under current circumstances in a population leads to realistic expectations and appropriate policy implementation. Countries with a large gap between current CPR and maximum CPR can focus on removing blocks to contraceptive use, while countries where the maximum potential CPR is near the actual CPR may need to shift their focus to demand generation or postpartum family planning programs. With a focus on equality of access to family planning, MCM produces CPR for all women, regardless of marital status. This paper details the mathematical construction of the MCM. A version of the model is available online for easy use by non-technical audiences in English and French.

Keywords

Contraception, Family Planning, Goal Setting, Advocacy

Corresponding author: Kristin E Bietsch

Competing interests: No competing interests were disclosed.

Grant information: This work was supported by The Bill & Melinda Gates Foundation [OPP1192802].
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Copyright: © 2020 Bietsch KE and Sonneveldt E. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Bietsch KE and Sonneveldt E. The Maximum CPR Model: a demographic tool for family planning policy [version 2; peer review: 2 approved]. Gates Open Res 2020, 3:1736 (https://doi.org/10.12688/gatesopenres.13094.2) First published: 31 Dec 2019, 3:1736 (https://doi.org/10.12688/gatesopenres.13094.1) Latest published: 19 Feb 2020, 3:1736 (https://doi.org/10.12688/gatesopenres.13094.2)

Revised Amendments from Version 1

We thank the reviewers for their comments and have addressed them in the revised version of our article. This new version includes more information on the assumptions made when creating the model and discusses which assumptions and defaults the users of the model may wish to alter. A table of the Maximum CPR and survey CPR for 61 countries is included. We have also produced code (available in our Zenodo repository) which allows users to calculate the maximum CPR for a single country using parity specific birth intervals.

See the authors' detailed response to the review by Philip Anglewicz
See the authors' detailed response to the review by John Ross and Jane T Bertrand

Introduction

The Maximum CPR Model (MCM) allows demographers, policy makers, and family planning advocates to determine a country’s highest potential contraceptive prevalence rate (CPR), based on an ideal number of children, key demographic life events, and structure of the population. Understanding the highest potential level of CPR achievable under current circumstances in a population leads to realistic expectations and appropriate policy implementation. Countries with a large gap between current CPR and maximum CPR can focus on removing blocks to contraceptive use, while countries where the maximum potential CPR is near the actual CPR may need to shift their focus to demand generation or postpartum family planning programs. With a focus on equality of access to family planning, MCM produces CPR for all women, regardless of marital status. This paper details the mathematical construction of the MCM. A version of the model is available online for easy use by non-technical audiences (Bietsch & Sonneveldt, 2020)¹, with default data preloaded from countries’ most recent Demographic and Health Surveys (DHS)² (Figure 1).

Figure 1.The online maximum CPR Model.

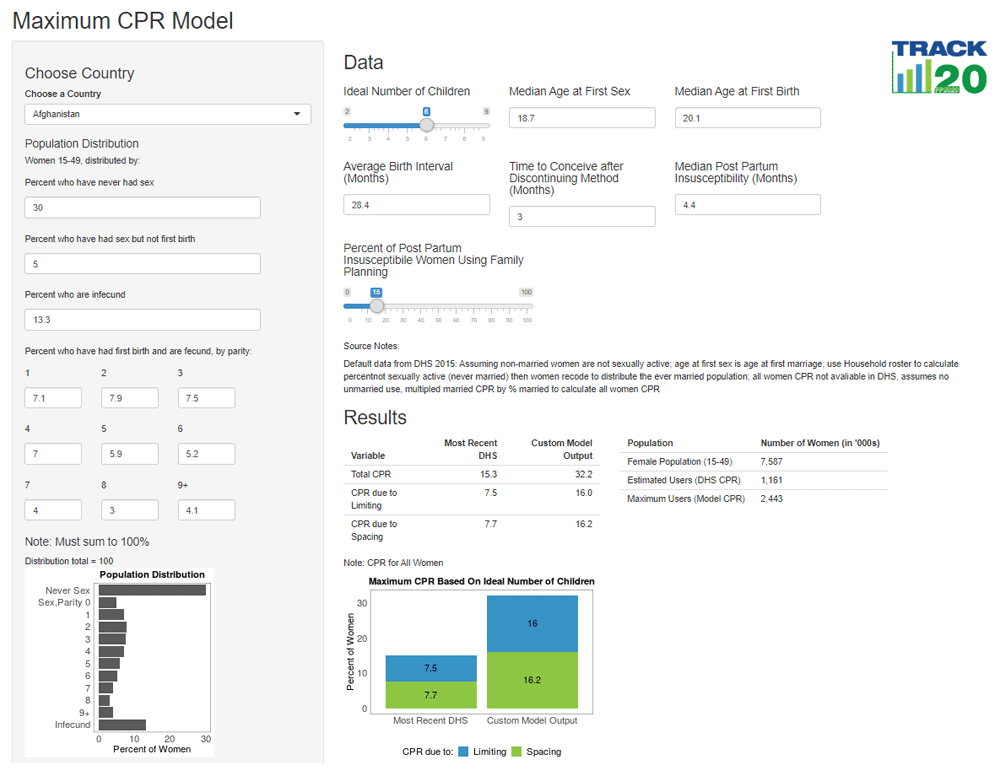
An interactive version of this plot can be viewed here: https://track20.shinyapps.io/maximum_cpr/.

The paper is structured as follows: the underlying equations and assumptions of the MCM, the model’s policy applications, especially regarding goal setting for Family Planning 2020 and beyond, and the relationship between the MCM and other models and measures of contraceptive use.

Methods

Maximum contraceptive prevalence calculations

The MCM finds the highest level of current use of contraception possible in a population if all women of reproductive age are using contraception when sexually active, unless they are actively trying to conceive³, already pregnant, postpartum infecund (some women use family planning while postpartum, which is also incorporated into the model⁴), or infecund, while trying to achieve a given level of fertility, based on the ideal number of children⁵. The model is composed of two pieces: the reproductive life course and the distribution of women into reproductive stages. At each stage of a woman’s life the model estimates what proportion of that period she would need contraception. Combining the life course with the population distribution data, we can estimate the maximum CPR for the population.

Five periods of the reproductive life course

In this model, the reproductive life course runs from ages 15 to 49 and is separated into 5 time periods:

P₁: Time between age 15 and first sex
P₂: Time between first sex and first birth
P₃: Time between first birth and last birth
P₄: Time between last birth and becoming infecund/menopausal⁶
P₅: Time between becoming infecund/menopausal and age 49

The reproductive life course can be summarized as:

R e p r o d u c t i v e L i f e = \sum_{i = 1}^{5} P_{i} (1)

Contraceptive use varies by period. In a population, women are distributed among the five stages. Therefore, the maximum CPR of a population is a function of the distribution of the population and the maximum contraceptive use at each stage of the reproductive life course.

{}_{\max}C P R = \sum_{i = P_{1}}^{P_{5}} C^{i} ⋅ D^{i} (2)

Cⁱ: Maximum contraceptive use in P_i
Dⁱ: Proportion of reproductive age women in P_i

Contraceptive use by period of the reproductive life course

Period 1: time between age 15 and first sex

We assume that in the first period, from 15 to becoming sexually active⁷, no one is using contraception⁸.

C^{P_{1}} = 0 (3)

This assumption potentially underestimates contraceptive use if women start using contraception in anticipation of coital activities.

Period 2: time between first sex and first birth

If we assume women use contraception until they explicitly wish to conceive, then this period is divisible into three sections: risk of unplanned pregnancy (where contraception could be used), time spent trying to conceive, and pregnancy. To calculate the length of this period, we use the median age at first sex⁹ and the median age at first birth¹⁰.

M^{P_{2}} = (A^{F B} − A^{F S}) \cdot 12 (4)

M^P₂: Months in Period 2
A^FB: Median age at first birth (Years)
A^FS: Median age at first sex (Years)

We must take into account that not all pregnancies result in live births. For this model, we assume that 10% of recognized pregnancies end in miscarriage or stillbirth (hence referred to as miscarriage) (American College of Obstetricians & Gynecologists, 2018), and the median length of pregnancy at termination is 3 months¹¹. We do not assume any abortions in this model, as CPR would be at its maximum in the absence of abortions¹².

To calculate the total number of pregnancies needed to achieve the ideal number of children, we must take into account the number of miscarriages. To calculate the time in each birth interval lost to miscarriage, we take the ideal number of children, divided by the proportion of pregnancies that result in a live birth to calculate the total number of pregnancies needed to obtain the ideal number of live births.

T P = \frac{I N C}{1 - P P M} (5)

TP: Total number of pregnancies needed to achieve ideal number of children
INC: Ideal number of children
PPM: Proportion of pregnancies ending in miscarriage

In this model, we assume PPM=0.1.

The lifetime number of miscarriages is the difference between number of pregnancies and number of births. The lifetime months spent on non-viable pregnancies is the average time to conception, plus 3 (the median length of pregnancy), multiplied by the number of terminations. The time spent for each birth interval is then the total months divided by the ideal number of children.

T M = T P − I N C (6)

TM: Total number of miscarriages

M^{T M} = (M^{C o n c e i v e} + M^{M i s c a r r i a g e}) ⋅ T M (7)

M^TM: Lifetime months spent on miscarriages
M^Conceive: Months to conceive
M^Miscarriage: Average duration of pregnancy at time of miscarriage

In this model, we assume M^Miscarriage=3.

M^{M_{B I}} = \frac{M^{T M}}{I N C} (8)

M^M_BI: Months spent on miscarriage per birth interval

The time trying to conceive¹³ varies by country. To calculate, we use the contraceptive calendar included in many DHS. Women who stop using a method are asked the reason for discontinuation, one answer being “discontinued to become pregnant.” For these women, we calculate the average time between discontinuation and pregnancy. Across countries, the time varied from 3 to 12 months¹⁴. For countries without calendar data, we use the median value across countries: 6 months.

We assume a length of pregnancy of 9 months.

Therefore, the maximum proportion of time in P₂ where women could use contraception is the number of months in P₂ not spent trying to conceive, pregnant, or with a miscarriage, divided by the total number of months in P₂.

C^{P_{2}} = \frac{M^{P_{2}} − M^{C o n c e i v e} − M^{P r e g n a n t} − M^{M_{B I}}}{M^{P_{2}}} (9)

M^Pregnant: Months pregnant

In this model, we assume M^Pregnant=9.

Women using in this period are classified as using to space, as no country with a DHS has an ideal number of children of 0¹⁵.

Period 3: Time between first birth and last birth

P₃ is made up of periods of closed birth intervals. P₃ is similar to P₂ in that it includes a time at risk, time trying to conceive, time pregnant, and time lost to miscarriages. However, it also includes a time of postpartum insusceptibility (PPI) following a birth. While some women do not use family planning at this time, others may take part in postpartum family planning (PPFP)¹⁶. The default assumption of the model is to use the current level of postpartum family planning, but users may edit this assumption to better understand how a postpartum family planning program can increase contraceptive use without a change in the ideal number of children.

The length of the birth interval is determined by the average birth interval in the country, and the total length of P₃ is the number of birth intervals (the number of ideal children minus one) multiplied by the average birth interval¹⁷. Time trying to conceive and pregnant are calculated the same way as they were in P₂.

M^{P_{3}} = M^{P_{3}^{B I}} ⋅ (I N C - 1) (10)

M^{P_{3}^{B I}} = M^{B I} (11)

M^P₃: Months in Period 3
$M^{P_{3}^{B I :}}$ Months in Period 3, per birth interval
M^BI: Average birth interval (months)

The length of PPI is the median duration from the DHS. To estimate PPFP use, DHS microdata is used to calculate¹⁸ the percent of women who are currently using family planning out of women who are postpartum infecund (either are practicing postpartum abstinence or are postpartum amenorrheic)¹⁹.

M^{C_{P P I}} = C^{P P I} ⋅ M^{P P I} (12)

M^C_PPI: Months contracepting during postpartum period
C^PPI: Percent of postpartum women using family planning
M^PPI: Average time postpartum infecund (months)

For the entirety of P₃, the maximum proportion of time where women could use contraception is the number of months in P₃ not spent postpartum infecund and not using contraception, trying to conceive, pregnant, or with a miscarriage, divided by the total number of months in P₃.

C^{P_{3}} = \frac{[M^{P_{3}^{B I}} − (M^{P P I} − M^{C_{P P I}}) − M^{C o n c e i v e} − M^{P r e g n a n t} − M^{M_{B I}}] \cdot [I N C − 1]}{M^{P_{3}^{B I}} ⋅ [I N C − 1]} (13)

Which simplifies to:

C^{P_{3}} = \frac{M^{P_{3}^{B I}} − (M^{P P I} − M^{C_{P P I}}) − M^{C o n c e i v e} − M^{P r e g n a n t} − M^{M_{B I}}}{M^{P_{3}^{B I}}} (14)

Women using in this period are classified as using to space.

Period 4: Time between last birth and becoming infecund/menopausal

While some women continue childbearing in their 50s, the DHS and other surveys assume most childbearing ends at 49. Ideally, we would calculate a median age at infecundity/menopause to close this period, but because most surveys do not have an age group that surpasses 50% infecund/menopausal, this calculation is impossible. For P₄, we assume that women remain fecund to 50. We will account for infecundity in the next period and in the population distribution. We assume that a woman’s last birth is also her last pregnancy, since she has reached the ideal number of children. Therefore, time lost to miscarriage is not included in Period 4.

M^{P_{4}} = (50 − A^{L B}) \cdot 12 (15)

M^P₄: Months in Period 4
A^LB: Age at last birth (years)

To calculate the expected age at last birth, we use the age at first birth, the number of birth intervals to achieve desired family size, and the average birth interval length.

A^{L B} = A^{F B} + \frac{[M^{B I} ⋅ (I N C − 1)]}{12} (16)

After the last birth, there is only postpartum insusceptibility and risk. Therefore, the maximum proportion of time where women could use contraception is the number of months in P₄ not spent postpartum infecund and not using contraception divided by the total number of months in P₄.

C^{P_{4}} = \frac{M^{P_{4}} − (M^{P P I} − M^{C_{P P I}})}{M^{P_{4}}} (17)

Women using in this period are classified as using to limit.

Period 5: Time between becoming infecund/menopausal and age 49

As with P₁, we do not believe women who are infecund or menopausal will use family planning.

C^{P_{5}} = 0 (18)

Summary: Contraceptive use by period of the reproductive life course

We now have equations defining maximum contraceptive use during the 5 periods of the reproductive life course, Table 1 summarizes the equations.

Table 1. Contraceptive use at each stage of the reproductive life course.

Description	Maximum contraceptive use
Time between age 15 and first sex	$C^{P_{1}} = 0$
Time between first sex and first birth	$C^{P_{2}} = \frac{M^{P_{2 −}} M^{C o n c e i v e} − M^{P r e g n a n t} − M^{M_{B I}}}{M^{P_{2}}}$
Time between first birth and last birth	$C^{P_{3}} = \frac{M^{P_{3}^{B I}} − (M^{P P I} − M^{C_{P P I}}) − M^{C o n c e i v e} − M^{P r e g n a n t} − M^{M_{B I}}}{M^{P_{3}^{B I}}}$
Time between last birth and becoming infecund/menopausal	$C^{P_{4}} = \frac{M^{P_{4}} − (M^{P P I} − M^{C_{P P I}})}{M^{P_{4}}}$
Time between becoming infecund/menopausal and age 49	$C^{P_{5}} = 0$

Population distribution

We distribute the population of women of reproductive age into the following groups²⁰.

D_{15}^{49} = {\begin{cases} D_{NS} = Percent of women who have never had sex \\ D_{0} = Percent of women who have had sex but not first birth \\ D_{1} = Percent of women at parity 1 \\ D_{2} = Percent of women at parity 2 \\ D_{3} = Percent of women at parity 3 \\ D_{4} = Percent of women at parity 4 \\ D_{5} = Percent of women at parity 5 \\ D_{6} = Percent of women at parity 6 \\ D_{7} = Percent of women at parity 7 \\ D_{8} = Percent of women at parity 8 \\ D_{9} = Percent of women at parity 9 + \\ D_{I} = Percent of women who are infecund \end{cases} (19)

Infecundity is determined using the same classifications as described in the DHS definition of Unmet Need (Bradley et al., 2012).

The population is collapsed into the following groups shown in Table 2, corresponding with the periods of the reproductive life course.

Table 2. Population distribution in the reproductive life course.

Description	Distribution by period	Population distribution
Never sexually active	D^P₁	D_NS
Nulliparous spacers	D^P₂	D₀
Parous spacers	D^P₃	$\sum_{p = 1}^{I N C - 1} D_{p}$
Limiters	D^P₄	$\sum_{p = I N C}^{9} D_{p}$
Infecund	D^P₅	D_I

As the ideal number of children changes, D₁ - D₉ shift between P₃ and P₄. D^P₃ will include parous, fecund women with at least one less child than the ideal number of children, and D^P₄ will include women at the parity of the ideal number of children and above. Note that in this model, ideal number of children is measured at the population level and is rounded to a whole number.

This model employs averages and medians at the population level. In many instances within a population, women at the same parity will have different ideal numbers of children. We assume that if a population was to achieve a fertility level of the average ideal number of children of its reproductive age women and had the maximum level of contraceptive use, on average, women below this parity would be using to space, and women above would be using to limit.

MCM

The maximum CPR of a population can thus be defined as the summation of the maximum CPR at each period of the reproductive life course multiplied by the proportion of the population of women of reproductive age in each period.

{}_{max}C P R = \sum_{i = P_{1}}^{P_{5}} C^{i} \cdot D^{i} (20)

The CPR can be separated into CPR for spacing and limiting as follows:

{}_{max}C P R_{s p a c i n g} = \sum_{i = P_{2}}^{P_{3}} C^{i} ⋅ D^{i} (21)

{}_{max}C P R_{L i m i t i n g} = C^{P_{4}} ⋅ D^{P_{4}} (22)

Results and discussion

Policy implications of the MCM

Understanding the highest potential level of CPR achievable under current circumstances in a population leads to realistic expectations and appropriate policy implementation. The following sections detail the policy relevant outputs and inputs of the MCM. While data from a recent survey can be used to estimate the current Maximum CPR, users may also create alternative scenarios by changing input values. To facilitate scenario creations for non-technical audiences, the authors have developed an online tool (in English and French) to implement and visualize the MCM²¹.

Outputs of MCM

Users of the MCM may find the model helpful for both understanding current situations and alternative scenarios. Policy makers looking to set contraceptive use goals can begin with the default data from a recent DHS and compare their country’s current CPR to the maximum CPR. Countries with large gaps between the current CPR and maximum CPR may be interested in exploring why such a gap exists, if there are barriers preventing women from accessing or using contraception²². If only a small gap exists between the current CPR and maximum CPR, countries will need to explore the inputs of the model and see if any would be appropriate for policy interventions. Table 3 shows the maximum CPR (based off default data) and survey CPR for the countries included in the online model.

Table 3. Maximum CPR with Default Data and Survey CPR.

Country and Survey Year	Survey CPR	Maximum CPR
Afghanistan 2015	15.3	32.2
Albania 2017-18	33.2	46.7
Angola 2015-16	13.3	28.5
Armenia 2015-16	36.7	38.3
Bangladesh 2014	44.2	62.3
Benin 2017-18	14.4	32.9
Bolivia 2008	41.3	56.8
Burkina Faso 2010	15.3	25.4
Burundi 2016-17	17.9	31.7
Cambodia 2014	38.5	44.4
Cameroon 2011	23.7	26.9
Chad 2014-15	5.4	11.1
Colombia 2015	64.9	66.9
Comoros 2012	13.7	29.9
Congo 2011-12	44.3	43.5
Congo Democratic Republic 2013-14	19.3	28.9
Cote d'Ivoire 2011-12	19.7	37.3
Dominican Republic 2013	55.1	59.9
Egypt 2014	40.8	52.2
Ethiopia 2016	25.3	36.9
Gabon 2012	33.6	40.4
Gambia 2013	7.1	18.8
Ghana 2014	22.8	45.3
Guatemala 2014-15	39.4	45.4
Guinea 2012	8.5	17.8
Haiti 2016-17	24.1	51.8
Honduras 2011-12	48.8	54.1
India 2015-16	40.8	51.7
Indonesia 2012	45.7	51.0
Jordan 2017-18	28.4	35.3
Kenya 2014	42.6	50.1
Kyrgyz Republic 2012	24.4	33.4
Lesotho 2014	48.9	54.3
Liberia 2013	21.7	36.8
Madagascar 2008-09	31.7	36.6
Malawi 2015-16	46.0	48.3
Maldives 2016-17	13.3	36.0
Mali 2012-13	9.9	28.5
Mozambique 2011	27.4	32.3
Myanmar 2015-16	31.6	44.6
Namibia 2013	50.2	53.2
Nepal 2016	40.8	59.2
Niger 2012	12.5	16.7
Nigeria 2013	16.0	31.0
Pakistan 2017-18	21.8	36.6
Peru 2012	51.5	63.3
Philippines 2017	33.6	40.7
Rwanda 2014-15	30.9	46.0
Sao Tome and Principe 2008-09	30.7	51.8
Senegal 2017	19.9	28.2
Sierra Leone 2013	22.1	31.2
South Africa 2016	48.2	57.9
Tajikistan 2017	21.3	36.8
Tanzania 2015-16	32.4	41.6
Timor-Leste 2016	16.1	25.1
Togo 2013-14	19.3	42.0
Turkey 2013	49.6	47.5
Uganda 2016	30.3	38.1
Yemen 2013	20.5	38.5
Zambia 2013-14	35.1	43.8
Zimbabwe 2015	48.6	50.1

By allowing maximum CPR to be separated into CPR_Spacing and CPR_Limiting, countries can better plan for the different types of contraceptive counseling needed by women who are interested in spacing or limiting births²³.

Many countries set goals for family planning as part of the FP2020 Global Initiative (Family Planning 2020, n.d.). As of May 2019, Track20 had collected information from 43 countries and converted goals²⁴ into all women mCPR²⁵. We compare the goals set by countries to the maximum CPR calculated using default data from the most recent DHS for the 37 goal setting countries with data.

In total, 16 countries have FP2020 goals higher than the Maximum CPR given the demographic characteristics in their most recent DHS. Of the 16 countries, 11 have goals within 5 percentage points of the maximum CPR. Some of these goals may be achievable if changes in inputs took place, such as increases in postpartum family planning or declines in ideal number of children. Guinea, Madagascar, Ethiopia, Malawi, and Niger are the five countries with the largest gap between their FP2020 goals and their current maximum CPR: in Malawi there is a 12.5 percentage point gap, and in Niger a 31.2 percentage point gap. While countries want to set ambitious goals to motivate investments and support, setting unrealistically high goals can demoralize policy implementors. As the global community looks forward past the end of the 2020 initiative to 2030 and beyond, the MCM can help policy makers set ambitious targets, both given their current demographic landscape and potential future scenarios.

After calculating the maximum CPR (or several based off different inputs), users can input the maximum CPR or a lower CPR into FamPlan, part of the Spectrum software (Avenir Health, 2019), to calculate a wide range of policy relevant data, such as the costs associated with increasing contraceptive use and the number of unintended pregnancies averted.

Inputs of MCM

Several inputs of the MCM may be of interest for policy makers. These include the ideal number of children, postpartum family planning, age at first sex and birth, and the average birth interval.

Ideal number of children: By changing the ideal number of children, the user changes how much of a woman’s reproductive life she will spend on childbearing, how much contraception she would need for spacing, and how much she would need for limiting. Changing the ideal number of children is not a simple policy intervention.
Percent of postpartum insusceptible women using family planning: Changing this number will change the use of family planning for spacing (and to a lesser extent, for limiting). Shifting the percent using PPFP allows users to see the impact of either no, some, or a large postpartum family planning program on the overall population’s CPR.
Age at first sex and first birth: If a policy goal is to delay the age at first birth, users may want to see the impact of increasing the period between first sex and first birth. If the period becomes significantly larger, users may want to adjust the distribution of women to have a larger share of their population sexually active, but nulliparous.
Average Birth Interval: Many health programs stress the importance of appropriately spaced births. The maximum CPR for spacing, will increase as birth intervals increase.

MCM compared to other models and measures of contraceptive use

Proximate Determinants of Fertility. The Proximate Determinants of Fertility Model, originally proposed by Bongaarts (1978) (and a simplification of a framework discussed by Davis & Blake (1956)), shares many similarities to the MCM, with notable differences. The Proximate Determinants of Fertility includes exposure to sexually activity (originally defined as percent married), contraception, induced abortion, lactational infecundability, frequency of intercourse, sterility, spontaneous intrauterine mortality, and duration of the fertile period. The main difference between the two models is the outcome of interest: contraceptive use for the MCM and the total fertility rate (TFR) for the Proximate Determinants of Fertility. Another important difference is that the Proximate Determinants of Fertility (and TFR) is age standardized, while there is no age standardization in MCM, in fact the population distribution is a key input. MCM uses ideal number of children, not TFR, because of a desire for the model to focus on a rights-based approach to family planning: the output should be read as how high can CPR grow while women are achieving their desired family size. While abortion is a key limiting factor of a population’s TFR in Bongaarts’ model, the MCM does not include induced abortion because it assumes CPR will be maximized when abortions are minimized. Lactation infecundability is included in both models, with MCM focusing on postpartum family planning as a keep input. MCM does not include a measure of frequency of intercourse, though Bongaarts says that it is easily demonstrated that coital frequency is not a very important determinant of fertility differences between populations, and does not include coital frequency in his mathematical equations. Intrauterine mortality is included in MCM as a constant (10% of pregnancies), and is discussed in Bongaarts’ model, though not thought to vary much between population. It is also not included in his mathematical equations. In summary, the Maximum CPR follows many assumptions of fertility limitations of the Proximate Determinants of Fertility, with changes to address the goals of MCM’s output.

Unmet need for family planning. Some may believe that the maximum contraceptive use in a population is the currently level of contraceptive use plus unmet need for family planning (The DHS Program, n.d.), but this is not the case. MCM is a current status measure, taking into account both the reproductive life course and current population distribution. Unmet need is composed of current status for some women, and retrospective status for others. Pregnant and postpartum amenorrheic women can be defined as having unmet need based on the intention status of their current/recent pregnancy. In MCM, they would not be included in the group of potential current contraceptive users. Thus, it is not uncommon for a survey CPR and unmet need, when added together, to surpass the maximum CPR estimated by the model.

The Demand Curve. The Demand Curve (Weinberger et al., 2017) looks at the ideal number of children and current modern contraceptive use in a country to determine if a country should consider increased investments in access or demand interventions. The Demand Curve is an equation calculated off the highest CPR witnessed in countries at give ideal number of children. We have conducted a comparison between the MCM with default data from recent DHS and Demand Curve, and present results in Figure 2.

Figure 2. Comparing demand curve with Maximum CPR Model.

The MCM results are shown in red and are close to the demand line for most countries with an ideal number of children of 3 or higher. We do not expect the results of lower fertility areas to overlap- research of the Demand Curve indicates that for countries with an ideal number of children below 3, there is no curve as in these countries it is assumed that fertility intentions are not limiting mCPR growth. There are numerous cases where the maximum CPR is higher than the demand curve, this is because the demand curve is based on historical observations, while MCM is a theoretical maximum, which most countries never have or will obtain. Figure 2 also shows the range MCM can take for the same ideal number of children: at 4 children, the maximum CPR ranges from 25% to 52%, highlighting the importance of other demographic indicators in determining a country’s room for contraceptive growth.

Conclusions

The MCM combines the reproductive life course and the structure of the population to produce the theoretical maximum current level of contraception for a population. This model is of particular interest to policy makers who can use it to set ambitious but achievable family planning goals. An online version of the model with built in default data, input adaptability, and graphic result displays aims to make demographic information as easily accessible as possible to technical and non-technical audiences. In a spirit of open research, all equations used in the calculations of the model outputs are available in this paper and a technical note on the Track20 website. Additionally, Stata files used to calculate default data are also available online. Technical support for users of the model is available through the Track20 team. The goal of the MCM is to make family planning modeling and goal setting available to all, in the hopes that demographic data will be more frequently included in informed policies.

Data availability

Underlying data

Users can enter their own data into the MCM. Default data for the most recent DHS is calculated by the authors and preloaded into the online model; default data will be updated periodically as new surveys are released.

The datasets used to generate the Maximum CPR Model are available in the MEASURE DHS repository (http://www.measuredhs.com). Access to the dataset requires registration and is granted to those that wish to use the data for legitimate research purposes. A guide for how to apply for dataset access is available at: https://dhsprogram.com/data/Access-Instructions.cfm.

Software availability

An online version of the MCM is available in English: https://track20.shinyapps.io/maximum_cpr/.

A French-language version is available at: https://track20.shinyapps.io/tpc_maximum/.

Source code used to create the model is available: https://github.com/kristinbietsch/MaxCPR/tree/v1.0.1.

Archived source code at time of publication: https://doi.org/10.5281/zenodo.3636183

License: MIT License.

Acknowledgements

We would like to thank Win Brown, Michelle Weinberger, and Edward Berchick for their thoughtful comments on earlier drafts.

Footnotes

¹In English: https://track20.shinyapps.io/maximum_cpr/ and French: https://track20.shinyapps.io/tpc_maximum/

²The online model also includes an option to start with an empty scenario- ideal for subnational analysis or for countries that have not had a recent DHS

³The model assumes that there is no ambivalence towards pregnancy- women are either actively trying to avoid pregnancy or become pregnant. In populations with a high share of women expressing ambivalence towards becoming pregnant, we would not except the CPR to be as high as the maximum CPR because women with ambivalence towards pregnancy are less likely to use contraception than women who are not ambivalent and do not want to become pregnant (Schwarz et al., 2007).

⁴We do not assume all postpartum women are using contraception- the ability to adjust the percent of women using family planning while postpartum insusceptible is a key component of the model

⁵The ideal family size in this model is the population average. Women may have fewer or more children than the ideal family size, and they also may have fewer or more children than their own ideal family size. It is not uncommon in DHS to find women who have higher than their ideal family size planning to have additional children. The model assumes that on average when women reach the parity of the population average ideal family size, they will move from being birth spacers to birth limiters.

⁶Not all, or even a majority of women are infecund by age 49, but in many countries it is a sizable portion of the population

⁷No recent DHS has a median age at first sex below 15

⁸Some women may use contraception before first sex or may use contraception and misreport sexual activity. In all 61 countries included in the default data for the model, less than 3% of women who have never had sex are using contraception at the time of interview, and in 56 countries, less than 1% use contraception.

⁹For women aged 25–49. If a user of the model believes that women in a survey are misreporting age at first sex, they can adjust the age downward.

¹⁰For women aged 25–49

¹¹Based on authors’ analysis of DHS calendar data

¹²We do not account for unwanted pregnancies due to contraceptive failures in this model

¹³We assume that the time to conceive does not vary by pregnancy outcome

¹⁴The countries with long periods spent trying to conceive are generally from surveys with small sample size of women reporting discontinuing in order to become pregnant, and these women are often not representative of the population. For countries with time to conceive over 10 months, we suspect biases in this measure and assume an average length of 6 months. This measure of time to conception is imperfect and potentially biased in both directions- women who explicitly discontinue contraception in order to conceive may be extremely motivated to become pregnant and monitor their cycles and time intercourse to become pregnant faster. Alternatively, women who discontinue to become pregnant are older than women who become pregnant without explicitly discontinuing contraception in 43 out of 45 surveys in our analysis with available data, and thus may experience decreased fecundability and longer times to conception (Larsen & Vaupel, 1993).

¹⁵The lowest ideal number of children in a DHS was 2.0 in Ukraine in 2007

¹⁶Technically, the maximum CPR would include all postpartum women using family planning, but this is unrealistic as many postpartum women are protected against pregnancy, and a minority of countries see postpartum family planning above 50% at 12 months postpartum (Winfrey & Rakesh, 2014)

¹⁷The average birth interval is itself determined by previous contraceptive use- we choose the average birth interval in this model as the assumed desired spacing between children. If a user of this model believes that birth intervals will increase in a country because of changing norms around healthy birth spacing, they could increase the number used for the average birth interval- this will increase the maximum CPR for spacing. For advanced users, R code to calculate MCM with parity specific birth intervals is available in the Zenodo repository for this paper.

¹⁸Stata Do files for indicators not available through Statcompiler are available in the Zenodo repository for this paper.

¹⁹Note that this measure of PPFP is different from other measures of PPFP which generally look at postpartum use at a given time after birth, as measured in the contraceptive calendar. For this model, PPFP is a current status measure, and tells, of all PPI women, what percent are currently using family planning

²⁰Note, the groups are mutually exclusive. Infecund women come from all parities, are excluded from D₁ - D₉, and combined together to create D_I

²¹In English: https://track20.shinyapps.io/maximum_cpr/ and French: https://track20.shinyapps.io/tpc_maximum/

²²The FPGoals Model (Track20, n.d.) would be a useful next step for policy makers in prioritizing interventions for increasing contraceptive use.

²³Choe & Bulatao (1992) believe that the appropriate method mix is determined by the distribution of women of reproductive age (in the same vein of the MCM), health implications of methods, and individual’s preferences.

²⁴Goals set by countries vary in form, such as by population (married or unmarried), measure (CPR or mCPR), and end date.

²⁵Maximum CPR is equivalent to the maximum mCPR if there is no traditional method use. We include all methods in the model, and do not differentiate by effectiveness.

Faculty Opinions recommended

References

American College of Obstetricians and Gynecologists: ACOG Practice Bulletin No. 200: Early Pregnancy Loss. Obstet Gynecol.2018; 132(5): e197–207. PubMed Abstract | Publisher Full Text
Avenir Health: Spectrum Manual: Spectrum System of Policy Models. 2019. Reference Source
Bietsch K, Sonneveldt E: Kristinbietsch/MasCPR CPR Model with Reviews February 2020. Zenodo. 2020. http://www.doi.org/10.5281/ZENODO.3636183
Bongaarts J: A Framework for Analyzing the Proximate Determinants of Fertility. Popul Dev Rev. 1978; 4(1): 105–32. Publisher Full Text
Bradley SEK, Croft TN, Fishel JD, et al.: Revising Unmet Need for Family Planning. DHS Analytical Studies No. 25. Calverton, Maryland, USA : ICF International. 2012. Reference Source
Choe MK, Bulatao RA: Defining an Appropriate Contraceptive Method Mix. Paper presented at Population Association of America Annual Meeting. Denver, Colorado. 1992. Reference Source
Davis K, Blake J: Social Structure and Fertility: An Analytic Framework. Econ Dev Cult Change. 1956; 4(3): 211–35. Publisher Full Text
Family Planning 2020: Commitments. Accessed December 5, 2019. Reference Source
Larsen U, Vaupel JW: Hutterite fecundability by age and parity: strategies for frailty modeling of event histories. Demography. 1993; 30(1): 81–102. PubMed Abstract | Publisher Full Text
Schwarz EB, Lohr PA, Gold MA, et al.: Prevalence and correlates of ambivalence towards pregnancy among nonpregnant women. Contraception. 2007; 75(4): 305–310. PubMed Abstract | Publisher Full Text
The DHS Program: Unmet Need for Family Planning. Accessed December 5, 2019. Reference Source
Track20: FP Goals. Accessed December 5, 2019. Reference Source
Weinberger M, Sonneveldt E, Stover J: The maximum contraceptive prevalence 'demand curve': guiding discussions on programmatic investments [version 1; peer review: 1 approved, 2 approved with reservations]. Gates Open Res. 2017; 1: 15. PubMed Abstract | Publisher Full Text | Free Full Text
Winfrey W, Rakesh K: Use of Family Planning in the Postpartum Period. DHS Comparative Report No. 36. Rockville, Maryland, USA: ICF International. 2014. Reference Source

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 31 Dec 2019

Author details Author details

¹ Avenir Health, Glastonbury, Connecticut, 06033, USA

Kristin E Bietsch
Roles: Conceptualization, Data Curation, Formal Analysis, Methodology, Software, Writing – Original Draft Preparation

Emily Sonneveldt
Roles: Conceptualization, Funding Acquisition, Methodology, Project Administration, Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

This work was supported by The Bill & Melinda Gates Foundation [OPP1192802].
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Article Versions (2)

version 2

Revised

Published: 19 Feb 2020, 3:1736

https://doi.org/10.12688/gatesopenres.13094.2

version 1

Published: 31 Dec 2019, 3:1736

https://doi.org/10.12688/gatesopenres.13094.1

© 2020 Bietsch KE and Sonneveldt E. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
Gates Open Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

SEE MORE DETAILS

CITE

how to cite this article

Bietsch KE and Sonneveldt E. The Maximum CPR Model: a demographic tool for family planning policy [version 2; peer review: 2 approved]. Gates Open Res 2020, 3:1736 (https://doi.org/10.12688/gatesopenres.13094.2)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Version 2

VERSION 2

PUBLISHED 19 Feb 2020

Revised

Views

113

Reviewer Report 24 Feb 2020

John Ross, Independent demographic consultant, New Orleans, USA

Jane T Bertrand, Department of Health Policy and Management, Tulane School of Public Health and Tropical Medicine, New Orleans, LA, USA

Approved

https://doi.org/10.21956/gatesopenres.14281.r28593

CITE

Report a concern

Respond or Comment

Views

Reviewer Report 20 Feb 2020

Philip Anglewicz, Department of Population, Family and Reproductive Health, Johns Hopkins Bloomberg School of Public Health, Baltimore, MD, USA

Approved

https://doi.org/10.21956/gatesopenres.14281.r28592

The authors have addressed my concerns. I ... Continue reading

CITE

Report a concern

Respond or Comment

Version 1

VERSION 1

PUBLISHED 31 Dec 2019

Views

Reviewer Report 20 Jan 2020

John Ross, Independent demographic consultant, New Orleans, USA

Jane T Bertrand, Department of Health Policy and Management, Tulane School of Public Health and Tropical Medicine, New Orleans, LA, USA

Approved with Reservations

https://doi.org/10.21956/gatesopenres.14251.r28407

I am submitting comments on this paper from two reviewers: my own (on the importance of this tool for countries developing objectives for their family planning programs) and those of John Ross, whom I asked to assist in assessing the calculations behind the model.

Comments from Jane Bertrand on the importance of this tool:

I cannot overstate the potential value of this tool for countries attempting to establish a realistic objective in terms of reaching a given level of contraceptive prevalence by a given date. Since the London Summit in 2012, many countries - especially in sub-Saharan Africa - have been encouraged to develop a strategic plan to reach a specific level of contraceptive use. The results of such efforts have yielded mixed results: some countries proposed realistic targets, others (seemingly believing it would be preferable to be wildly optimistic) proposed unattainable targets. When, in the latter case, countries fall considerably short of meeting the target, the local leadership can become very discouraged, which is precisely the opposite motivation that setting an objective was intended to bring. This tool will be useful in assisting countries to better understand what is feasible, given the specific country context.

Comments from John Ross on the computations presented in the article:

The model is quite novel and it takes a little while to wrap one’s mind around it. So --- the maximum CPR occurs when everyone uses a method who should be doing so --- she wants to avoid pregnancy, and she is fully exposed to it by being fully fecund (i.e. not pregnant, or with PPI, or sterile, etc.). That gets compared to the actual CPR so planners can explore reasons for the gap.

The starting base is cross-sectional, a snapshot for the five life stages. But the user can explore effects through time with alternative inputs that reflect future assumptions. So that is useful.

At the start the text says there is no allowance for abortions since “CPR would be at its maximum in the absence of abortions” apparently because abortions occupy some reproductive time during which those women could be users. But that is true of miscarriages also --- so why not input a higher figure than the 10% for miscarriages, or say that if you wish you can input a higher figure for your country of interest. The net effect would be to lower the maximum CPR. So under equation 5, line 4, that would increase the adjustment of 0.1 for the proportion of miscarriages.

In Period 4, after the last birth, there is some contraceptive use. The maximum time for that in equation 17 is not quite explicit. It should subtract the total time for all subsequent miscarriages or abortions. So the calculation seems to need an estimate of the pregnancy rate in the open period after the final birth, to get the time lost.

I wish that the average birth intervals in equations 10 and 11 were parity specific, since the average is affected by the mix of women by birth interval, and the longer the interval the higher the max CPR. That varies by country and through time, and it would be nice to be able to enter detailed interval lengths.

A conceptual problem I think is that the heavy reliance on the birth interval doesn’t recognise that it is itself due partly to past use. Perhaps that’s OK --- the main purpose is to get the total length of Stage 3 by the average interval length times the number of intervals (= to the ideal family size minus one). But the average birth interval is elongated by past use, so the total for Stage 3 is lengthened. So the estimate of total time in Stage 3 is too long if past use were omitted, or it is too short if all past intervals had had the maximum CPR. (Just asking.)

Stage 3 is short for a Taiwan, making Stage 4 long; the reverse occurs for a Niger. All use is labelled as spacing in Stage 3, and limiting in Stage 4. Of course no model can do everything but under “limitations” it’s perhaps worth mentioning that it’s not ideal to have no limiters between the first and last births, since many limiters exist within every birth interval, having accidental pregnancies and births, and many use IUDs or implants. Similarly, in Stage 4 many women who wish to limit rely on short term methods. Equations 21 and 22 do separate the CPR by spacing and limiting; perhaps a suggestion could be made on how these might be modified from survey information on the spacing/limiting split by birth interval, or some such.

A real plus is the focus on the CPR, not the sorely limited MCPR. The inclusion of traditional methods is important; maybe there’s room for a footnote that they can be intended as either a spacing or limiting method and that they are unique by their high failure rates.

Other limitations -- median values are used for age at first sex, age at first birth, the average birth interval, and PPI; again no model can do everything, and in the end the estimated gaps between the maximum and actual CPRs will still lead to useful planning discussions.

Finally, equating the final birth to the ideal family size works in the model, but it appears to be for the population average, whereas it varies considerably by women’s age and parity, and the text should clarify that.

As a side note, much non use is actually due to not being married, but that’s covered by starting with first sex and first birth.

The text should say that this model can be linked to other models by using the maximum CPR as inputs. That would speak to its focus just on contraception.

Perhaps worth mentioning that Choe and Bulatao¹ years ago prescribed “appropriate” use according to life stages. Galway and Stover also worked on an “appropriate mix.” Galway K, and Stover J. Determining an appropriate contraceptive method mix,” chapter 2 in Anon., Policy and Programmatic Use of DHS Data: A Tool for Family Planning Program Managers and Analysts. The Futures Group OPTIONS II Project. 1995.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Partly
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Partly

References

1. Chloe MK, Bulatao RA: Defining an appropriate contraceptive method mix to meet fertility preferences. 1992 Annual Meeting of the Population Association of America. 1992.

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Implementation of family planning programs in LMIC; monitoring and evaluation of such programs.

We confirm that we have read this submission and believe that we have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however we have significant reservations, as outlined above.

CITE

Report a concern

Author Response 19 Feb 2020

Kristin Bietsch, Avenir Health, Glastonbury, 06033, USA

19 Feb 2020

Author Response
Thank you both for your thoughtful comments. We have made considered all your suggestions and made several changes to our article following your review:
- We find the parity
... Continue reading
Thank you both for your thoughtful comments. We have made considered all your suggestions and made several changes to our article following your review:

We find the parity specific birth interval discussion very interesting. For a general user of the model, they could change the average birth interval if they believed there would be a change over time as birth spacing became more common. For more advanced user, we have created a parity specific birth interval version of the model and wrote R code to calculate the maximum CPR for a single country. We have included the R code in the Github repository for this paper.

We have added a discussion on how birth intervals are influenced by contraceptive use. We use the average birth interval as the “desired spacing between children” and discuss how it might change with programs that encourage birth spacing.

We have added a discussion on how individual women will vary from the population averages which underlie the model- especially in regard to ideal family size. We have also analyzed several DHS and found that many women report using to space or unmet need for spacing when already at or above their personal ideal number of children- suggesting that the ideal number of children is not a ceiling. Therefore, while the model may classify women as limiters, they may see themselves as spacers. We have edited the paper to discuss how the model’s breakdown of use for spacing and limiting may be beneficial for contraceptive counseling. We choose to use ideal number of children in our model instead or the total fertility rate to focus on contraceptive growth without restricting reproductive rights.

We have included reference to Choe and Bulasto’s work on how countries can determine an appropriate method mix.

We added a footnote discussing traditional methods and how the model does not differentiate contraceptive use by efficacy.

We have added to the policy section how users may find it useful to take the results of their maximum CPR scenarios and input these numbers into FamPlan, part of the Spectrum Software, to calculated costs and benefits of certain levels of CPR.

We did not include abortions with miscarriages in our model because there are different times to conception. Since the model assumes that women use contraception until wishing to become pregnant, there would be very few unplanned pregnancies (only those resulting from method failure). Miscarriages would result from planned pregnancies, so the model includes not only the duration of the pregnancy but also the time to conception in the time lost because of miscarriages. Abortions would have no time to conception. We chose not to include abortions in the model because in a population where everyone uses contraception, the number of abortions would be low, and the share of the reproductive life spent with these pregnancies would be small. We also chose not to allow users of the online model to vary the proportion of pregnancies that are miscarried because of lack of policy interventions. If an advanced user believed that the share of miscarriages was much higher in a population, the model code is available online and can be modified.

We have added in our discussion of Period 4 that the last birth is also the last pregnancy when maximizing CPR, as women who reach this last birth become users of contraception in order to limit and would not have additional miscarriages.
Thank you both for your thoughtful comments. We have made considered all your suggestions and made several changes to our article following your review:

We find the parity specific birth interval discussion very interesting. For a general user of the model, they could change the average birth interval if they believed there would be a change over time as birth spacing became more common. For more advanced user, we have created a parity specific birth interval version of the model and wrote R code to calculate the maximum CPR for a single country. We have included the R code in the Github repository for this paper.

We have added a discussion on how birth intervals are influenced by contraceptive use. We use the average birth interval as the “desired spacing between children” and discuss how it might change with programs that encourage birth spacing.

We have added a discussion on how individual women will vary from the population averages which underlie the model- especially in regard to ideal family size. We have also analyzed several DHS and found that many women report using to space or unmet need for spacing when already at or above their personal ideal number of children- suggesting that the ideal number of children is not a ceiling. Therefore, while the model may classify women as limiters, they may see themselves as spacers. We have edited the paper to discuss how the model’s breakdown of use for spacing and limiting may be beneficial for contraceptive counseling. We choose to use ideal number of children in our model instead or the total fertility rate to focus on contraceptive growth without restricting reproductive rights.

We have included reference to Choe and Bulasto’s work on how countries can determine an appropriate method mix.

We added a footnote discussing traditional methods and how the model does not differentiate contraceptive use by efficacy.

We have added to the policy section how users may find it useful to take the results of their maximum CPR scenarios and input these numbers into FamPlan, part of the Spectrum Software, to calculated costs and benefits of certain levels of CPR.

We did not include abortions with miscarriages in our model because there are different times to conception. Since the model assumes that women use contraception until wishing to become pregnant, there would be very few unplanned pregnancies (only those resulting from method failure). Miscarriages would result from planned pregnancies, so the model includes not only the duration of the pregnancy but also the time to conception in the time lost because of miscarriages. Abortions would have no time to conception. We chose not to include abortions in the model because in a population where everyone uses contraception, the number of abortions would be low, and the share of the reproductive life spent with these pregnancies would be small. We also chose not to allow users of the online model to vary the proportion of pregnancies that are miscarried because of lack of policy interventions. If an advanced user believed that the share of miscarriages was much higher in a population, the model code is available online and can be modified.

We have added in our discussion of Period 4 that the last birth is also the last pregnancy when maximizing CPR, as women who reach this last birth become users of contraception in order to limit and would not have additional miscarriages.
Competing Interests: None to report Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 19 Feb 2020

Kristin Bietsch, Avenir Health, Glastonbury, 06033, USA

19 Feb 2020

Author Response
Thank you both for your thoughtful comments. We have made considered all your suggestions and made several changes to our article following your review:
- We find the parity
... Continue reading
Thank you both for your thoughtful comments. We have made considered all your suggestions and made several changes to our article following your review:

We find the parity specific birth interval discussion very interesting. For a general user of the model, they could change the average birth interval if they believed there would be a change over time as birth spacing became more common. For more advanced user, we have created a parity specific birth interval version of the model and wrote R code to calculate the maximum CPR for a single country. We have included the R code in the Github repository for this paper.

We have added a discussion on how birth intervals are influenced by contraceptive use. We use the average birth interval as the “desired spacing between children” and discuss how it might change with programs that encourage birth spacing.

We have added a discussion on how individual women will vary from the population averages which underlie the model- especially in regard to ideal family size. We have also analyzed several DHS and found that many women report using to space or unmet need for spacing when already at or above their personal ideal number of children- suggesting that the ideal number of children is not a ceiling. Therefore, while the model may classify women as limiters, they may see themselves as spacers. We have edited the paper to discuss how the model’s breakdown of use for spacing and limiting may be beneficial for contraceptive counseling. We choose to use ideal number of children in our model instead or the total fertility rate to focus on contraceptive growth without restricting reproductive rights.

We have included reference to Choe and Bulasto’s work on how countries can determine an appropriate method mix.

We added a footnote discussing traditional methods and how the model does not differentiate contraceptive use by efficacy.

We have added to the policy section how users may find it useful to take the results of their maximum CPR scenarios and input these numbers into FamPlan, part of the Spectrum Software, to calculated costs and benefits of certain levels of CPR.

We did not include abortions with miscarriages in our model because there are different times to conception. Since the model assumes that women use contraception until wishing to become pregnant, there would be very few unplanned pregnancies (only those resulting from method failure). Miscarriages would result from planned pregnancies, so the model includes not only the duration of the pregnancy but also the time to conception in the time lost because of miscarriages. Abortions would have no time to conception. We chose not to include abortions in the model because in a population where everyone uses contraception, the number of abortions would be low, and the share of the reproductive life spent with these pregnancies would be small. We also chose not to allow users of the online model to vary the proportion of pregnancies that are miscarried because of lack of policy interventions. If an advanced user believed that the share of miscarriages was much higher in a population, the model code is available online and can be modified.

We have added in our discussion of Period 4 that the last birth is also the last pregnancy when maximizing CPR, as women who reach this last birth become users of contraception in order to limit and would not have additional miscarriages.
Thank you both for your thoughtful comments. We have made considered all your suggestions and made several changes to our article following your review:

We find the parity specific birth interval discussion very interesting. For a general user of the model, they could change the average birth interval if they believed there would be a change over time as birth spacing became more common. For more advanced user, we have created a parity specific birth interval version of the model and wrote R code to calculate the maximum CPR for a single country. We have included the R code in the Github repository for this paper.

We have added a discussion on how birth intervals are influenced by contraceptive use. We use the average birth interval as the “desired spacing between children” and discuss how it might change with programs that encourage birth spacing.

We have added a discussion on how individual women will vary from the population averages which underlie the model- especially in regard to ideal family size. We have also analyzed several DHS and found that many women report using to space or unmet need for spacing when already at or above their personal ideal number of children- suggesting that the ideal number of children is not a ceiling. Therefore, while the model may classify women as limiters, they may see themselves as spacers. We have edited the paper to discuss how the model’s breakdown of use for spacing and limiting may be beneficial for contraceptive counseling. We choose to use ideal number of children in our model instead or the total fertility rate to focus on contraceptive growth without restricting reproductive rights.

We have included reference to Choe and Bulasto’s work on how countries can determine an appropriate method mix.

We added a footnote discussing traditional methods and how the model does not differentiate contraceptive use by efficacy.

We have added to the policy section how users may find it useful to take the results of their maximum CPR scenarios and input these numbers into FamPlan, part of the Spectrum Software, to calculated costs and benefits of certain levels of CPR.

We did not include abortions with miscarriages in our model because there are different times to conception. Since the model assumes that women use contraception until wishing to become pregnant, there would be very few unplanned pregnancies (only those resulting from method failure). Miscarriages would result from planned pregnancies, so the model includes not only the duration of the pregnancy but also the time to conception in the time lost because of miscarriages. Abortions would have no time to conception. We chose not to include abortions in the model because in a population where everyone uses contraception, the number of abortions would be low, and the share of the reproductive life spent with these pregnancies would be small. We also chose not to allow users of the online model to vary the proportion of pregnancies that are miscarried because of lack of policy interventions. If an advanced user believed that the share of miscarriages was much higher in a population, the model code is available online and can be modified.

We have added in our discussion of Period 4 that the last birth is also the last pregnancy when maximizing CPR, as women who reach this last birth become users of contraception in order to limit and would not have additional miscarriages.
Competing Interests: None to report Close
Report a concern

Views

Reviewer Report 20 Jan 2020

Philip Anglewicz, Department of Population, Family and Reproductive Health, Johns Hopkins Bloomberg School of Public Health, Baltimore, MD, USA

Approved with Reservations

https://doi.org/10.21956/gatesopenres.14251.r28405

This research is important and interesting. Overall, the approach is clear, structured, and sound. The authors also do well in describing the value of this concept for FP planning, as this may lead to more realistic target MCPRs

This research is important and interesting. Overall, the approach is clear, structured, and sound. The authors also do well in describing the value of this concept for FP planning, as this may lead to more realistic target MCPRs for countries.
The main challenges with this approach seems to be that some fairly rigid assumptions are required but don’t reflect the imprecision and ambiguity involved in childbearing preferences and behaviors.

For example, It’s not exactly an unreasonable assumption that no one is using contraception prior to first sex, but it’s possible to assess the validity of this assumption. For DHS countries, what percentage of not sexually active women aged 15 or over are using contraception? An underlying challenge here is that sexual activity among young unmarried women is under-reported, which implies that assuming no contraceptive use for this group would underestimate the maximum CPR (which, as the authors state, is already likely underestimated for this group).

Also, the assumption that women “assume women use contraception until they explicitly wish to conceive” is questionable in light of research on the large body of research on childbearing ambivalence, which is fluctuates over the life course. So there probably isn’t a clear and measurable distinction between risk of unplanned pregnancy and time spent trying to conceive. Similarly, women who state that they discontinued contraceptive use specifically in order to get pregnant might be more determined to get pregnant and therefore may be more successful to do so, which might mean that the actual time trying to conceive is underestimated. In addition, women who are ambivalent about pregnancy may be more likely to not use, so they perhaps should be counted as potential users.
Although the purpose of this research is to describe the method for calculating the maximum CPR, it would be interesting and useful to see values of this for selected countries, along with the actual CPR, and the CPR goal stated for each country, which might highlight the utility of this concept.
Figure 2: it would be useful to also see the average MCM for each ideal number of children across countries, in addition to the distribution.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Partly

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Demography, family planning, contraceptive use, research methods.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

CITE

Report a concern

Author Response 19 Feb 2020

Kristin Bietsch, Avenir Health, Glastonbury, 06033, USA

19 Feb 2020

Author Response
Thank you for your thoughtful comments and suggestions. We have updated our paper in the following ways:
- Regarding contraceptive use among women who have never had sex, we
... Continue reading
Thank you for your thoughtful comments and suggestions. We have updated our paper in the following ways:

Regarding contraceptive use among women who have never had sex, we looked at the 61 surveys included in the model and found that in most cases no women who reported never having sex also reported currently using contraception. In all countries, less than 3% reported using contraception, and in 56 countries less than 1% reported contraceptive use. We believe that numbers this small would not affect the maximum CPR calculations.

We agree with the reviewer’s comment that women may misreport sexual activity and age at first sex. We have added to a footnote about median age at first sex that if a user of the model believes the median age in the survey is biased, they can adjust the number down in the interactive online model.

The reviewer makes an excellent point that the model does not consider ambiguity of pregnancy intentions. We have added to the paper a discussion of how ambiguity would limit CPR growth to lower than the maximum CPR since research has found women who are ambivalent about pregnancy are less likely to use contraception. Policy makers should take the level of uncertainty, which varies greatly in the surveys included in our analysis, into account when creating goals for CPR growth.

We have added a footnote discussing how time to conception may be biased- we believe in either direction. As the reviewer points out, women who stop using contraception to become pregnant may become pregnant more quickly than other women because of motivation to time intercourse with ovulation. The authors believe time to conception may actually be biased in the opposite direction as well- we analyzed DHS surveys with available data and found in 43 out of 45 surveys women who discontinue to become pregnant are older than women who became pregnant without discontinuing contraception for that purpose. The older women may experience decreased fecundity and thus longer times to conception. We have noted both potential biases in the paper, and users of the model are free to edit the input as they see fit.

We have included a table in the latest draft of the survey CPR and maximum CPR for 61 countries. We did not include country FP2020 goals because of variability in how the goals were set, the timeframes to meeting the goals, and the population the goals apply to.

We have added the average maximum CPR for each ideal number of children in Figure 2.
Thank you for your thoughtful comments and suggestions. We have updated our paper in the following ways:

Regarding contraceptive use among women who have never had sex, we looked at the 61 surveys included in the model and found that in most cases no women who reported never having sex also reported currently using contraception. In all countries, less than 3% reported using contraception, and in 56 countries less than 1% reported contraceptive use. We believe that numbers this small would not affect the maximum CPR calculations.

We agree with the reviewer’s comment that women may misreport sexual activity and age at first sex. We have added to a footnote about median age at first sex that if a user of the model believes the median age in the survey is biased, they can adjust the number down in the interactive online model.

The reviewer makes an excellent point that the model does not consider ambiguity of pregnancy intentions. We have added to the paper a discussion of how ambiguity would limit CPR growth to lower than the maximum CPR since research has found women who are ambivalent about pregnancy are less likely to use contraception. Policy makers should take the level of uncertainty, which varies greatly in the surveys included in our analysis, into account when creating goals for CPR growth.

We have added a footnote discussing how time to conception may be biased- we believe in either direction. As the reviewer points out, women who stop using contraception to become pregnant may become pregnant more quickly than other women because of motivation to time intercourse with ovulation. The authors believe time to conception may actually be biased in the opposite direction as well- we analyzed DHS surveys with available data and found in 43 out of 45 surveys women who discontinue to become pregnant are older than women who became pregnant without discontinuing contraception for that purpose. The older women may experience decreased fecundity and thus longer times to conception. We have noted both potential biases in the paper, and users of the model are free to edit the input as they see fit.

We have included a table in the latest draft of the survey CPR and maximum CPR for 61 countries. We did not include country FP2020 goals because of variability in how the goals were set, the timeframes to meeting the goals, and the population the goals apply to.

We have added the average maximum CPR for each ideal number of children in Figure 2.
Competing Interests: No competing interests Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 19 Feb 2020

Kristin Bietsch, Avenir Health, Glastonbury, 06033, USA

19 Feb 2020

Author Response
Thank you for your thoughtful comments and suggestions. We have updated our paper in the following ways:
- Regarding contraceptive use among women who have never had sex, we
... Continue reading
Thank you for your thoughtful comments and suggestions. We have updated our paper in the following ways:

Regarding contraceptive use among women who have never had sex, we looked at the 61 surveys included in the model and found that in most cases no women who reported never having sex also reported currently using contraception. In all countries, less than 3% reported using contraception, and in 56 countries less than 1% reported contraceptive use. We believe that numbers this small would not affect the maximum CPR calculations.

We agree with the reviewer’s comment that women may misreport sexual activity and age at first sex. We have added to a footnote about median age at first sex that if a user of the model believes the median age in the survey is biased, they can adjust the number down in the interactive online model.

The reviewer makes an excellent point that the model does not consider ambiguity of pregnancy intentions. We have added to the paper a discussion of how ambiguity would limit CPR growth to lower than the maximum CPR since research has found women who are ambivalent about pregnancy are less likely to use contraception. Policy makers should take the level of uncertainty, which varies greatly in the surveys included in our analysis, into account when creating goals for CPR growth.

We have added a footnote discussing how time to conception may be biased- we believe in either direction. As the reviewer points out, women who stop using contraception to become pregnant may become pregnant more quickly than other women because of motivation to time intercourse with ovulation. The authors believe time to conception may actually be biased in the opposite direction as well- we analyzed DHS surveys with available data and found in 43 out of 45 surveys women who discontinue to become pregnant are older than women who became pregnant without discontinuing contraception for that purpose. The older women may experience decreased fecundity and thus longer times to conception. We have noted both potential biases in the paper, and users of the model are free to edit the input as they see fit.

We have included a table in the latest draft of the survey CPR and maximum CPR for 61 countries. We did not include country FP2020 goals because of variability in how the goals were set, the timeframes to meeting the goals, and the population the goals apply to.

We have added the average maximum CPR for each ideal number of children in Figure 2.
Thank you for your thoughtful comments and suggestions. We have updated our paper in the following ways:

Regarding contraceptive use among women who have never had sex, we looked at the 61 surveys included in the model and found that in most cases no women who reported never having sex also reported currently using contraception. In all countries, less than 3% reported using contraception, and in 56 countries less than 1% reported contraceptive use. We believe that numbers this small would not affect the maximum CPR calculations.

We agree with the reviewer’s comment that women may misreport sexual activity and age at first sex. We have added to a footnote about median age at first sex that if a user of the model believes the median age in the survey is biased, they can adjust the number down in the interactive online model.

The reviewer makes an excellent point that the model does not consider ambiguity of pregnancy intentions. We have added to the paper a discussion of how ambiguity would limit CPR growth to lower than the maximum CPR since research has found women who are ambivalent about pregnancy are less likely to use contraception. Policy makers should take the level of uncertainty, which varies greatly in the surveys included in our analysis, into account when creating goals for CPR growth.

We have added a footnote discussing how time to conception may be biased- we believe in either direction. As the reviewer points out, women who stop using contraception to become pregnant may become pregnant more quickly than other women because of motivation to time intercourse with ovulation. The authors believe time to conception may actually be biased in the opposite direction as well- we analyzed DHS surveys with available data and found in 43 out of 45 surveys women who discontinue to become pregnant are older than women who became pregnant without discontinuing contraception for that purpose. The older women may experience decreased fecundity and thus longer times to conception. We have noted both potential biases in the paper, and users of the model are free to edit the input as they see fit.

We have included a table in the latest draft of the survey CPR and maximum CPR for 61 countries. We did not include country FP2020 goals because of variability in how the goals were set, the timeframes to meeting the goals, and the population the goals apply to.

We have added the average maximum CPR for each ideal number of children in Figure 2.
Competing Interests: No competing interests Close
Report a concern

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 31 Dec 2019

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2
Version 2 (revision) 19 Feb 20	read	read
Version 1 31 Dec 19	read	read

Philip Anglewicz, Johns Hopkins Bloomberg School of Public Health, Baltimore, USA
John Ross, Independent demographic consultant, New Orleans, USA

Jane T Bertrand, Tulane School of Public Health and Tropical Medicine, New Orleans, USA

Comments on this article

All Comments(0)

Add a comment

Back to all reports

Reviewer Report

113 Views

24 Feb 2020 | for Version 2

John Ross, Independent demographic consultant, New Orleans, USA

Jane T Bertrand, Department of Health Policy and Management, Tulane School of Public Health and Tropical Medicine, New Orleans, LA, USA

113 Views Cite this report Responses(0)

Approved

The authors have been quite responsive to each of the questions I raised before, with changes both in the text and in the model for advanced users.

One comment however: while they note at the start that this paper is devoted to the mathematical construction of the model, many readers may in a first reading be troubled, as I was, by the inattention to abortions. An explanation/defense of the abortion reasoning I think should be prominent in the Introduction as part of a brief perspective for the “layman” before diving into the equations. The next to last bullet in their list of responses, if paraphrased, could serve for that.

Otherwise the paper seems ready to go.

Competing Interests

No competing interests were disclosed.

We confirm that we have read this submission and believe that we have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

9 Views

20 Feb 2020 | for Version 2

Philip Anglewicz, Department of Population, Family and Reproductive Health, Johns Hopkins Bloomberg School of Public Health, Baltimore, MD, USA

9 Views Cite this report Responses(0)

Approved

The authors have addressed my concerns. I commend them on their interesting and important research.

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Demography, family planning, contraceptive use, research methods.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

21 Views

20 Jan 2020 | for Version 1

John Ross, Independent demographic consultant, New Orleans, USA

Jane T Bertrand, Department of Health Policy and Management, Tulane School of Public Health and Tropical Medicine, New Orleans, LA, USA

21 Views Cite this report Responses(1)

Approved With Reservations

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Partly
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Partly

References

1. Chloe MK, Bulatao RA: Defining an appropriate contraceptive method mix to meet fertility preferences. 1992 Annual Meeting of the Population Association of America. 1992.

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Implementation of family planning programs in LMIC; monitoring and evaluation of such programs.

Respond to this report

Responses (1)

Author Response

19 Feb 2020

Kristin Bietsch, Avenir Health, Glastonbury, 06033, USA

Thank you both for your thoughtful comments. We have made considered all your suggestions and made several changes to our article following your review:

We find the parity specific birth interval discussion very interesting. For a general user of the model, they could change the average birth interval if they believed there would be a change over time as birth spacing became more common. For more advanced user, we have created a parity specific birth interval version of the model and wrote R code to calculate the maximum CPR for a single country. We have included the R code in the Github repository for this paper.
We have added a discussion on how birth intervals are influenced by contraceptive use. We use the average birth interval as the “desired spacing between children” and discuss how it might change with programs that encourage birth spacing.
We have added a discussion on how individual women will vary from the population averages which underlie the model- especially in regard to ideal family size. We have also analyzed several DHS and found that many women report using to space or unmet need for spacing when already at or above their personal ideal number of children- suggesting that the ideal number of children is not a ceiling. Therefore, while the model may classify women as limiters, they may see themselves as spacers. We have edited the paper to discuss how the model’s breakdown of use for spacing and limiting may be beneficial for contraceptive counseling. We choose to use ideal number of children in our model instead or the total fertility rate to focus on contraceptive growth without restricting reproductive rights.
We have included reference to Choe and Bulasto’s work on how countries can determine an appropriate method mix.
We added a footnote discussing traditional methods and how the model does not differentiate contraceptive use by efficacy.
We have added to the policy section how users may find it useful to take the results of their maximum CPR scenarios and input these numbers into FamPlan, part of the Spectrum Software, to calculated costs and benefits of certain levels of CPR.
We did not include abortions with miscarriages in our model because there are different times to conception. Since the model assumes that women use contraception until wishing to become pregnant, there would be very few unplanned pregnancies (only those resulting from method failure). Miscarriages would result from planned pregnancies, so the model includes not only the duration of the pregnancy but also the time to conception in the time lost because of miscarriages. Abortions would have no time to conception. We chose not to include abortions in the model because in a population where everyone uses contraception, the number of abortions would be low, and the share of the reproductive life spent with these pregnancies would be small. We also chose not to allow users of the online model to vary the proportion of pregnancies that are miscarried because of lack of policy interventions. If an advanced user believed that the share of miscarriages was much higher in a population, the model code is available online and can be modified.
We have added in our discussion of Period 4 that the last birth is also the last pregnancy when maximizing CPR, as women who reach this last birth become users of contraception in order to limit and would not have additional miscarriages.

View more View less

Competing Interests

None to report

Back to all reports

Reviewer Report

22 Views

20 Jan 2020 | for Version 1

Philip Anglewicz, Department of Population, Family and Reproductive Health, Johns Hopkins Bloomberg School of Public Health, Baltimore, MD, USA

22 Views Cite this report Responses(1)

Approved With Reservations

This research is important and interesting. Overall, the approach is clear, structured, and sound. The authors also do well in describing the value of this concept for FP planning, as this may lead to more realistic target MCPRs for countries.
The main challenges with this approach seems to be that some fairly rigid assumptions are required but don’t reflect the imprecision and ambiguity involved in childbearing preferences and behaviors.

For example, It’s not exactly an unreasonable assumption that no one is using contraception prior to first sex, but it’s possible to assess the validity of this assumption. For DHS countries, what percentage of not sexually active women aged 15 or over are using contraception? An underlying challenge here is that sexual activity among young unmarried women is under-reported, which implies that assuming no contraceptive use for this group would underestimate the maximum CPR (which, as the authors state, is already likely underestimated for this group).

Also, the assumption that women “assume women use contraception until they explicitly wish to conceive” is questionable in light of research on the large body of research on childbearing ambivalence, which is fluctuates over the life course. So there probably isn’t a clear and measurable distinction between risk of unplanned pregnancy and time spent trying to conceive. Similarly, women who state that they discontinued contraceptive use specifically in order to get pregnant might be more determined to get pregnant and therefore may be more successful to do so, which might mean that the actual time trying to conceive is underestimated. In addition, women who are ambivalent about pregnancy may be more likely to not use, so they perhaps should be counted as potential users.
Although the purpose of this research is to describe the method for calculating the maximum CPR, it would be interesting and useful to see values of this for selected countries, along with the actual CPR, and the CPR goal stated for each country, which might highlight the utility of this concept.
Figure 2: it would be useful to also see the average MCM for each ideal number of children across countries, in addition to the distribution.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Partly

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Demography, family planning, contraceptive use, research methods.

Respond to this report

Responses (1)

Author Response

19 Feb 2020

Kristin Bietsch, Avenir Health, Glastonbury, 06033, USA

Thank you for your thoughtful comments and suggestions. We have updated our paper in the following ways:

Regarding contraceptive use among women who have never had sex, we looked at the 61 surveys included in the model and found that in most cases no women who reported never having sex also reported currently using contraception. In all countries, less than 3% reported using contraception, and in 56 countries less than 1% reported contraceptive use. We believe that numbers this small would not affect the maximum CPR calculations.
We agree with the reviewer’s comment that women may misreport sexual activity and age at first sex. We have added to a footnote about median age at first sex that if a user of the model believes the median age in the survey is biased, they can adjust the number down in the interactive online model.
The reviewer makes an excellent point that the model does not consider ambiguity of pregnancy intentions. We have added to the paper a discussion of how ambiguity would limit CPR growth to lower than the maximum CPR since research has found women who are ambivalent about pregnancy are less likely to use contraception. Policy makers should take the level of uncertainty, which varies greatly in the surveys included in our analysis, into account when creating goals for CPR growth.
We have added a footnote discussing how time to conception may be biased- we believe in either direction. As the reviewer points out, women who stop using contraception to become pregnant may become pregnant more quickly than other women because of motivation to time intercourse with ovulation. The authors believe time to conception may actually be biased in the opposite direction as well- we analyzed DHS surveys with available data and found in 43 out of 45 surveys women who discontinue to become pregnant are older than women who became pregnant without discontinuing contraception for that purpose. The older women may experience decreased fecundity and thus longer times to conception. We have noted both potential biases in the paper, and users of the model are free to edit the input as they see fit.
We have included a table in the latest draft of the survey CPR and maximum CPR for 61 countries. We did not include country FP2020 goals because of variability in how the goals were set, the timeframes to meeting the goals, and the population the goals apply to.
We have added the average maximum CPR for each ideal number of children in Figure 2.

View more View less

Competing Interests

No competing interests

Alongside their report, reviewers assign a status to the article:

Approved - the paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations - A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approved - fundamental flaws in the paper seriously undermine the findings and conclusions

[1] American College of Obstetricians and Gynecologists: ACOG Practice Bulletin No. 200: Early Pregnancy Loss. Obstet Gynecol.2018; 132(5): e197–207. PubMed Abstract | Publisher Full Text

[2] Avenir Health: Spectrum Manual: Spectrum System of Policy Models. 2019. Reference Source

[3] Bietsch K, Sonneveldt E: Kristinbietsch/MasCPR CPR Model with Reviews February 2020. Zenodo. 2020. http://www.doi.org/10.5281/ZENODO.3636183

[4] Bongaarts J: A Framework for Analyzing the Proximate Determinants of Fertility. Popul Dev Rev. 1978; 4(1): 105–32. Publisher Full Text

[5] Bradley SEK, Croft TN, Fishel JD, et al.: Revising Unmet Need for Family Planning. DHS Analytical Studies No. 25. Calverton, Maryland, USA : ICF International. 2012. Reference Source

[6] Choe MK, Bulatao RA: Defining an Appropriate Contraceptive Method Mix. Paper presented at Population Association of America Annual Meeting. Denver, Colorado. 1992. Reference Source

[7] Davis K, Blake J: Social Structure and Fertility: An Analytic Framework. Econ Dev Cult Change. 1956; 4(3): 211–35. Publisher Full Text

[8] Family Planning 2020: Commitments. Accessed December 5, 2019. Reference Source

[9] Larsen U, Vaupel JW: Hutterite fecundability by age and parity: strategies for frailty modeling of event histories. Demography. 1993; 30(1): 81–102. PubMed Abstract | Publisher Full Text

[10] Schwarz EB, Lohr PA, Gold MA, et al.: Prevalence and correlates of ambivalence towards pregnancy among nonpregnant women. Contraception. 2007; 75(4): 305–310. PubMed Abstract | Publisher Full Text

[11] The DHS Program: Unmet Need for Family Planning. Accessed December 5, 2019. Reference Source

[12] Track20: FP Goals. Accessed December 5, 2019. Reference Source

[13] Weinberger M, Sonneveldt E, Stover J: The maximum contraceptive prevalence 'demand curve': guiding discussions on programmatic investments [version 1; peer review: 1 approved, 2 approved with reservations]. Gates Open Res. 2017; 1: 15. PubMed Abstract | Publisher Full Text | Free Full Text

[14] Winfrey W, Rakesh K: Use of Family Planning in the Postpartum Period. DHS Comparative Report No. 36. Rockville, Maryland, USA: ICF International. 2014. Reference Source

The Maximum CPR Model: a demographic tool for family planning policy

Abstract

Keywords

Revised Amendments from Version 1

Introduction

Figure 1.The online maximum CPR Model.

Methods

Maximum contraceptive prevalence calculations

Five periods of the reproductive life course

Contraceptive use by period of the reproductive life course

Table 1. Contraceptive use at each stage of the reproductive life course.

Population distribution

Table 2. Population distribution in the reproductive life course.

MCM

Results and discussion

Policy implications of the MCM

Outputs of MCM

Table 3. Maximum CPR with Default Data and Survey CPR.

Inputs of MCM

MCM compared to other models and measures of contraceptive use

Figure 2. Comparing demand curve with Maximum CPR Model.

Conclusions

Data availability

Underlying data

Software availability

Acknowledgements

Footnotes

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Are you a Gates-funded researcher?

Thank you!

The Maximum CPR Model: a demographic tool for family planning policy

Abstract

Keywords

Revised Amendments from Version 1

Introduction

Figure 1.The online maximum CPR Model.

Methods

Maximum contraceptive prevalence calculations

Five periods of the reproductive life course

Contraceptive use by period of the reproductive life course

Table 1. Contraceptive use at each stage of the reproductive life course.

Population distribution

Table 2. Population distribution in the reproductive life course.

MCM

Results and discussion

Policy implications of the MCM

Outputs of MCM

Table 3. Maximum CPR with Default Data and Survey CPR.

Inputs of MCM

MCM compared to other models and measures of contraceptive use

Figure 2. Comparing demand curve with Maximum CPR Model.

Conclusions

Data availability

Underlying data

Software availability

Acknowledgements

Footnotes

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Competing Interests Policy

Stay Updated

Are you a Gates-funded researcher?

Thank you!