The Cascade Analysis Tool: software to analyze and optimize care cascades

David J Kedziora; Romesh Abeysuriya; Cliff C Kerr; George L Chadderdon; Vlad-Ștefan Harbuz; Sarah Metzger; David P Wilson; Robyn M Stuart

doi:10.12688/gatesopenres.13031.1

Home Browse The Cascade Analysis Tool: software to analyze and optimize care cascades

ALL Metrics

Views

Downloads

Get PDF

Get XML

Export

▬

✚

Software Tool Article

The Cascade Analysis Tool: software to analyze and optimize care cascades

[version 1; peer review: 3 approved with reservations]

David J Kedziora^1,2, Romesh Abeysuriya³, Cliff C Kerr¹, [...] George L Chadderdon⁴, Vlad-Ștefan Harbuz⁵, Sarah Metzger⁶, David P Wilson⁶, Robyn M Stuart ⁷

David J Kedziora^1,2, Romesh Abeysuriya³, [...] Cliff C Kerr¹, George L Chadderdon⁴, Vlad-Ștefan Harbuz⁵, Sarah Metzger⁶, David P Wilson⁶, Robyn M Stuart ⁷

PUBLISHED 07 Jun 2019

Author details Author details

¹ School of Physics, University of Sydney, Physics Rd, Camperdown, Sydney, NSW 2006, Australia
² Institute for Global Health, University College London, 30 Guilford Street, London, WC1N 1EH, UK
³ Monash University, 553 St Kilda Road, Melbourne, VIC 3004, Australia
⁴ Independent researcher, 72 Bayview Street, Prahran, VIC 3181, Australia
⁵ Phyramid, Südquaistrasse 14, Kleinhafen, Basel, 4057, Switzerland
⁶ Bill and Melinda Gates Foundation, 500 Fifth Avenue North, Seattle, WA, 98109, USA
⁷ Department of Mathematical Sciences, University of Copenhagen, Universitetsparken 5, Copenhagen, 2100, Denmark

David J Kedziora
Roles: Investigation, Methodology, Software, Writing – Review & Editing

Romesh Abeysuriya
Roles: Investigation, Methodology, Software, Writing – Review & Editing

Cliff C Kerr
Roles: Software, Visualization, Writing – Review & Editing

George L Chadderdon
Roles: Software, Visualization

Vlad-Ștefan Harbuz
Roles: Software, Visualization

Sarah Metzger
Roles: Project Administration, Writing – Review & Editing

David P Wilson
Roles: Conceptualization, Project Administration, Writing – Review & Editing

Robyn M Stuart
Roles: Funding Acquisition, Methodology, Project Administration, Software, Supervision, Writing – Original Draft Preparation, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS

Abstract

Introduction: Cascades, which track the progressive stages of engagement on the path towards a successful outcome, are increasingly being employed to quantitatively assess progress towards targets associated with health and development responses. Maximizing the proportion of people with successful outcomes within a budget-constrained context requires identifying and implementing interventions that are not only effective, but also cost-effective.
Methods: We developed a software application called the Cascade Analysis Tool that implements advanced analysis and optimization methods for understanding cascades, combined with the flexibility to enable application across a wide range of areas in health and development. The tool allows users to design the cascade, collate and enter data, and then use the built-in analysis methods in order to answer key policy questions, such as: understanding where the biggest drop-offs along the cascade are; visualizing how the cascade varies by population; investigating the impact of introducing a new intervention or scaling up/down existing interventions; and estimating how available funding should be optimally allocated among available interventions in order to achieve a variety of different objectives selectable by the user (such as optimizing cascade outcomes in target years). The Cascade Analysis Tool is available via a user-friendly web-based application, and comes with a user guide, a library of pre-made examples, and training materials.
Discussion: Whilst the Cascade Analysis Tool is still in the early stages of existence, it has already shown promise in preliminary applications, and we believe there is potential for it to help make sense of the increasing quantities of data on cascades.

Keywords

cascades, optimization, modeling, service delivery

Corresponding author: Robyn M Stuart

Competing interests: No competing interests were disclosed.

Grant information: This work was supported by the Bill and Melinda Gates Foundation [OPP1181918].
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Copyright: © 2019 Kedziora DJ et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Kedziora DJ, Abeysuriya R, Kerr CC et al. The Cascade Analysis Tool: software to analyze and optimize care cascades [version 1; peer review: 3 approved with reservations]. Gates Open Res 2019, 3:1488 (https://doi.org/10.12688/gatesopenres.13031.1) First published: 07 Jun 2019, 3:1488 (https://doi.org/10.12688/gatesopenres.13031.1) Latest published: 24 Dec 2019, 3:1488 (https://doi.org/10.12688/gatesopenres.13031.2)

Introduction

The pursuit of effective program delivery has become a dominant theme in the discussions and strategic thinking of both national and international health and development agencies. Both the Paris Declaration on Aid Effectiveness¹ and the Accra Agenda for Action² emphasized the need for results-based evaluation to assess whether funds are being used efficiently towards achieving desired outcomes, and this has played an important role in shaping the thinking around results measurement more broadly. To support the emphasis on results-based evaluation, a multitude of systems are in operation for collecting and aggregating program result data³. In theory, these data are intended to enable organizations to assess which strategies and programs are effective, identify elements of programs associated with better results, demonstrate accountability to external stakeholders, and make decisions about allocating further funding³. In practice, however, there is a disconnect between the data being collected and the methods available for analyzing them.

One method for quantifying how health and development programs are servicing the needs of communities is to define progressive stages of engagement on the path towards a successful outcome, and to measure what proportion of the overall target population has attained each stage. Often, these proportions are plotted as successive bars, in a representation known as a cascade, a care cascade or a service cascade (Figure 1). Cascades can be studied at a population level (left panel of Figure 1), or at a disaggregated sub-population level (right panel of Figure 1).

Figure 1. A typical cascade presents the proportion of the total target population that have attained each of the sequential steps of engagement in the path towards a successful outcome.

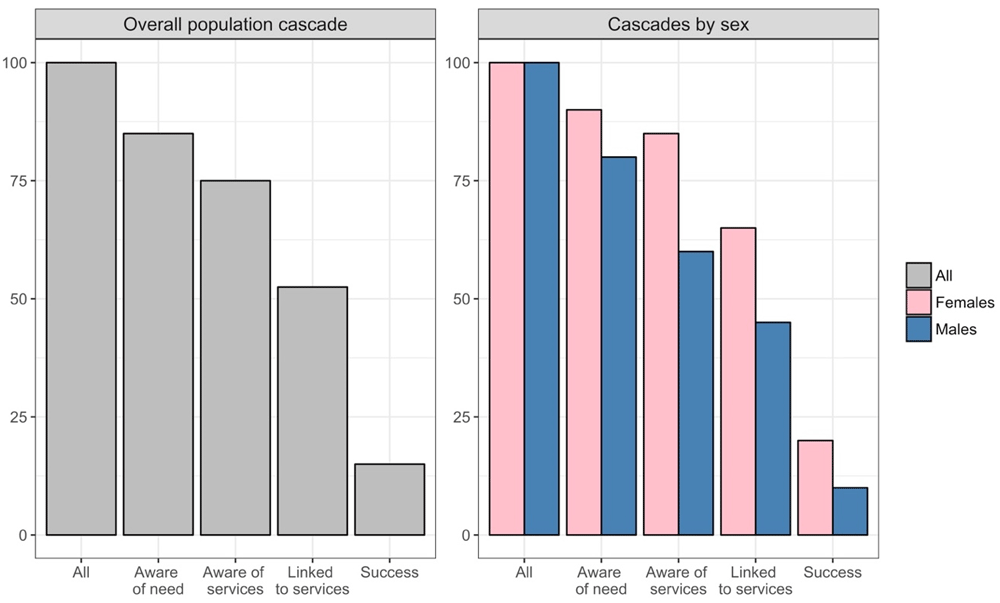
The left panel is aggregated across the total population, and the right panel shows the same information but disaggregated by sex.

Within public health, cascade-type models were explored as early as the 1960s for analyzing the success of tuberculosis programs⁴, but the concept of a cascade really gained traction within HIV⁵, where it is used to characterize the steps of care that people living with HIV go through. The HIV care cascade has been adopted in many countries as a population-level tool to evaluate the progress of individuals through the HIV care continuum^5–8. Following their success in HIV, cascades began to be applied to other areas of health. Tuberculosis followed soon after HIV, with the 2014 End TB Strategy including targets related to the latent tuberculosis cascade of care, and the following year’s Global Plan To End TB 2016–2020⁹ including a commitment to measure progress towards these targets. Subsequently, an explicit framework of analysis to account for the losses during each individual step in this cascade was developed¹⁰ and applied in South Africa¹¹, India¹² and many other countries. The cascade approach has also been applied to the analysis of diabetes, most notably in a 2014 study that provided a comprehensive overview of the continuum of U.S. diabetes care (including a visualization of gaps in awareness of diagnosis, engagement, and treatment) by analyzing nationally representative data benchmarked against care recommendations for cardiovascular risk management¹³. Building on this, a recent study in South Africa used data from the first comprehensive national survey on non-communicable diseases to construct a diabetes care cascade by categorizing the population with diabetes into those who were unscreened, screened but undiagnosed, diagnosed but untreated, treated but uncontrolled, and treated and controlled¹⁴. The cascade framework has also been proposed as an analytic tool in hepatitis C¹⁵, other sexually transmitted infections^16,17, addiction care^18,19, and mental health²⁰. Outside of public health, a related concept – funnel analyses – have proven useful in analyzing consumer behavior within ecommerce, retail, and online gaming/applications.

Across all of these different applications, cascades have proven to be an effective visual tool for identifying weaknesses at different stages of service engagement, as well as unacceptable variations between different groups or countries. In addition, a handful of studies have pushed the analytic capacity of cascades one step further, employing them as a tool for identifying what mix of technologies and services should be provided, and to which populations, in order to best ensure that outcomes are met. A study of the HIV cascade in Kenya looked at how varying the coverage levels of five different interventions could improve the care cascade²¹. An unpublished study conducted in South Africa further extended this idea, introducing the concept of ‘optimizing the cascade’, which meant calculating the coverage levels across 30+ HIV interventions that would maximize the number of people virally suppressed by 2030.

Although there are many prior examples of cascade analyses, and even a few specifically on cascade optimization, these have all been disease-specific use cases. The lack of a readily-available modelling tool has substantially limited the potential for widespread uptake of cascade analyses and cascade optimizations. The purpose of this work is to begin with the concept of a cascade and implement it as a general software tool – called the Cascade Analysis Tool – that allows the same quantitative methods to be applied across application areas in health and development. The Cascade Analysis Tool is intended to address a set of key policy questions, as outlined in Figure 2. Methodologically, it is based on a compartmental mathematical model structure equipped with methods for parameterizing transition probabilities, and with a suite of inbuilt optimization methods for ‘optimizing the cascade’; that is, finding the annual investment or coverage levels for each intervention that would result in the cascade being as close as possible to some target distribution, subject to constraints on the overall budget and the pace of scale-up over time.

Figure 2. The types of questions designed to be answered by the Cascade Analysis Tool.

The Cascade Analysis Tool is available as open access software package, developed in Python and available via GitHub. We also developed a graphical user interface to enable interested users to access the software via a web-based application. Throughout this paper, we refer to an illustrative example of a hypertension cascade; this example, along with several other pre-made models, are available to all users as part of the library of ‘demo’ projects included with the software.

The Cascade Analysis Tool is intended to provide a practical way for stakeholders to utilize the increasing quantities of data on the costs, coverage, and impact of health and development interventions, and modalities through which these interventions are delivered to individuals, thus addressing some of the disconnect between the kinds of data being collected and the methods available for analyzing them.

Methods

Implementation

The Cascade Analysis Tool is a web application written using the Atomica and Sciris packages. The Cascade Analysis Tool comes with a library of pre-made cascades that can be immediately used for analyses. Alternatively, users can design their own cascade (see details in the next section).

Operation

The Cascade Analysis Tool can be run on any browser. The workflow creating and analyzing a cascade in the Cascade Analysis Tool consists of three key steps: designing the cascade, collating data, and analysis. If using one of the pre-made cascades in the Cascade Analysis Tool’s library, it is possible to skip the first step.

Designing the cascade. The Cascade Analysis Tool is intended to be as flexible as possible, meaning that nothing about the cascade design is pre-determined. Thus, designing the cascade is the starting point for any cascade analysis. We will first show how a cascade can be represented as a compartmental model, and then provide details on how to set up a compartmental model representing a cascade within the Cascade Analysis Tool.

Representing a cascade as a compartmental model

Conceptually, the process of designing a cascade is illustrated in Figure 3. Beginning with a simple cascade representation, in which the progressive stages along the path to a successful outcome are plotted (Figure 3a), the next step is to break down each cascade bar so that it consists of the sum of all the bars that came before it, plus the difference between the height of the previous bars and the height of the current bar (Figure 3b). These differences represent the mutually exclusive states that a person can be in. This representation in terms of mutually exclusive states allows us to model the cascade using a compartmental model, which is one of the main workhorses for disease modeling in general. A compartmental model consists of a set of mutually exclusive states that a person can be in, plus a set of transitions between them (Figure 3c).

Figure 3. A generic treatment cascade (panel A), which is translated (panel B) into a compartmental model (panel C).

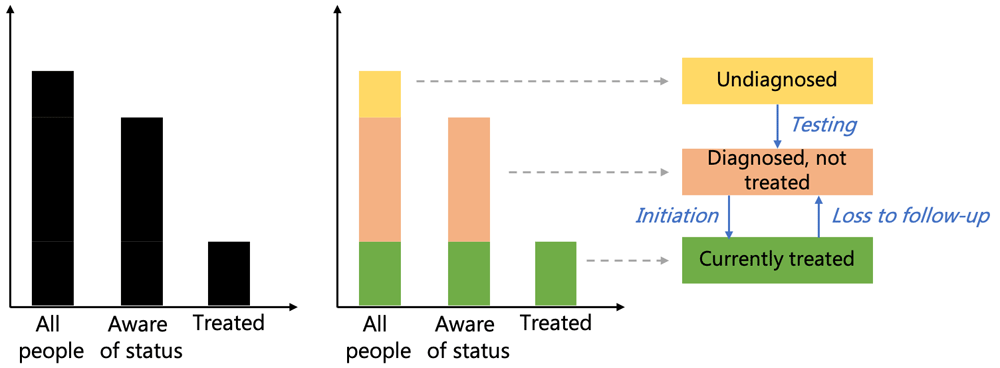
Creating a compartmental model

Having completed the conceptual stage of designing the cascade, resulting in a representation of the cascade as a compartmental model, users can then proceed to create their model in the Cascade Analysis Tool. This is done by creating a framework file, which is a Microsoft Excel spreadsheet containing the specifications of the model. A model consists of three mandatory components – compartments, transitions, and parameters. The framework also contains two additional optional quantities, characteristics and cascades, which facilitate data entry and analysis. The design of the cascade and the initial consideration of available data should often be carried out in parallel because the selection of quantities included in the model directly affects which quantities are required for data entry.

Compartments

Figure 3 illustrates the process of transforming a typical cascade representation into a set of compartments, labelled as “Undiagnosed”, “Diagnosed, not treated”, and “Currently treated” in Figure 3c. To set up a model using the Cascade Analysis Tool, the first step is to define these compartments in the framework file.

The selection of compartments is often driven by desired outputs, which in turn reflect available data. For example, if one of the aims of the cascade analysis is to assess barriers to diagnosis following screening, then there should be compartments for both screened individuals and diagnosed individuals. In contrast, if there is no screening step, if there are no interventions targeted to reduce barriers to diagnosis, or if screening is not relevant to the analysis at hand, then it may be sufficient to only have a compartment for diagnosed individuals.

Transitions

In Figure 3c, there are arrows between the compartments that illustrate the paths that people can take between different states. For example, people can go from “Undiagnosed” to “Diagnosed, not treated” after receiving a test, or from “Currently treated” to “Diagnosed, not treated” if they are lost from care. A pathway leading from one state to another is called a transition. Within the Cascade Analysis Tool, each transition is given a name and is defined as a function of one or more parameters.

Parameters

Parameters are used to define the values associated with transitions in the model. In the example presented in Figure 3, the parameters are the testing rate, the treatment initiation rate, and the loss-to-follow-up rate. A parameter can be associated with more than one transition – for example, the background death rate applies to all individuals regardless of their disease status. When using the Cascade Analysis Tool, users have a choice of either directly entering data on these parameters, or allowing their values to be calculated as a function of other model quantities (such as other parameters) by entering formulas into the framework file. This means that complex computations and functional dependencies can be readily used. The parameterization of the transitions needs to be carefully thought out with relation to the available data.

Characteristics

Characteristics are defined as groupings of model compartments. The most common use case would be to define each of the cascade stages as a characteristic. For example, in the model introduced in Figure 3, we would consider “Aware of status” to be a characteristic of the model, since it is the sum of two compartments. Specifying characteristics is optional – it is possible to set up a framework file that only contains compartments, transitions, and parameters – but characteristics are a useful way of summarizing information about the distribution of people in multiple different compartments, which is an essential part of a cascade analysis.

Collating data. The next key step in a cascade analysis is to collate data. Data collation is specific to a particular context, and users create a project for encapsulating all of the data and analyses specific to that context. Creating a project requires selecting the framework that will be used as the basis for the cascade model structure, selecting the number of populations to include, and selecting the years for which data will be collected. Data entry itself is done in two Excel spreadsheets, referred to as the databook and the program book, both of which are automatically created by the Cascade Analysis Tool once a project has been created. Within the databook, users enter data on each parameter that influences the rates at which people move through the cascade, and within the program book, they enter data on the interventions that influence the parameters. The Cascade Analysis Tool comes with a library of pre-filled databooks and program books that can be immediately used for demonstration analyses. The next section on use cases illustrates the process of data entry with reference to an example.

Analysis of policy questions. Having completed the cascade design and gathered the data, it is possible to begin using the framework to analyze policy questions, such as those illustrated in Figure 2. In many real-world situations, the impact of changing intervention coverage and the way in which interventions should be prioritized is not clear from an analysis of the intervention properties alone. The Cascade Analysis Tool allows users to construct scenarios and optimizations in order to quantitatively answer questions about intervention effects and priorities. Scenarios can be used within the Cascade Analysis Tool in order to assess the impact on the cascade of varying the investment or coverage level of a given intervention or modality.

Cascade optimization

Although scenarios are useful for analyzing cascades and for gaining insight on the impact of scaling up or down particular interventions or modalities, in realistic settings there are a very large number of different possibilities, and it quickly becomes infeasible to rely on constructing scenarios in order to determine what investment priorities should be. This is especially difficult given that the optimal investment strategy may change from year to year. For example, it might be optimal to start by scaling up treatment initiation services until everyone in need of treatment can access it, and then to focus investments on adherence and retention strategies subsequently.

The Cascade Analysis Tool contains a set of inbuilt optimization functions that can calculate the distribution of funding across service delivery modalities that results in the best possible cascade. ‘Best’ can be defined by the user – often, the aim is for as many people as possible to attain a successful outcome; in this case, the optimization algorithm would calculate the mix of investments that maximizes the proportion of the population with successful outcomes. However, it is also possible to specify different strategic goals, such as maximizing the number of people diagnosed. This functionality within the tool is primarily intended for central decision makers who are choosing the allocation of a budget. Fundamentally, the optimization system in the Cascade Analysis Tool seeks to modify the timing and funding allocation of interventions to optimize an aspect of the model outputs, subject to constraints on the changes it is allowed to make.

The optimization problem is separated into three components

The objective (i.e. defining what we are trying to achieve)
The adjustment(s) (i.e., what can be adjusted, and when, in order to meet the objectives)
Constraints (i.e., what conditions must be satisfied)

Separating these components out means they can be mixed-and-matched to suit a specific optimization problem. Finally, the optimization is numerically performed using one of several algorithms selectable by the user.

Objectives (i.e., what are we trying to achieve)?

The Cascade Analysis Tool allows the user to flexibly define objectives when designing the cascade. It also supports default options, as listed here:

Minimize the summed loss rates over each stage of the cascade
Maximize the number of people at any given stage of the cascade
Minimize the amount of funding required to meet a certain cascade target

It is possible for users to construct their own objective using any of the model’s outputs, as well as to combine multiple objectives into a single target.

Adjustment type (i.e., what can be adjusted, and when, in order to meet the objectives)?

The adjustments for an optimization are a specification of what is allowed to be changed in the model in order to achieve the optimal result. The Cascade Analysis Tool has several default options for possible adjustments

Immediate one-off allocation change: we ask what share of the annual budget should be allocated to each intervention in order to meet the objectives, subject to any constraints (see section below). The share of the budget allocated to each intervention is assumed to be constant over time, and we assume that the allocation of the budget can change immediately.
Delayed one-off allocation change: we ask what share of the annual budget should be allocated to each intervention in order to meet the objectives, subject to any constraints (see section below). The share of the budget allocated to each intervention is assumed to be constant over time, and we assume that the allocation of the budget can only change after a given year (for example, perhaps change can only take effect in the next planning phase).
Ongoing (time-varying) allocation changes: we ask what share of the annual budget should be allocated to each intervention in order to meet the objectives, subject to any constraints (see section below). The share of the budget allocated to each intervention is allowed to vary over time, according to a schedule defined by the user (for example, it may be possible to change the allocation every year, or every three years, etc.).
Start-year optimization: rather than varying the share of the budget allocated to each intervention, in this case we seek the optimal timing of making a budget reallocation, subject to any constraints (see section below).

Constraints (i.e., what conditions must be satisfied)?

Constraints limit possible options when optimizing. They serve as requirements that must be met by any proposed solution. The Cascade Analysis Tool has two principal types of constraint:

Constraints on individual adjustments: These typically set minimum or maximum amounts of funding that can be allocated to each intervention independently. These may be constant, or they may vary over time when optimizing scale-up or scale-down scenarios.
Constraining the total budget: there is an overall fixed budget, which is either assumed to be constant over time, or allowed to vary over time (e.g., annually).

Optimization algorithms

After defining the optimization, the tool produces an objective function that can be used to perform the numerical optimization using one of several different algorithms. The Cascade Analysis Tool has built-in support for the following algorithms:

Adaptive Stochastic Descent (ASD) implemented by the sciris Python package. This is a gradient-descent type optimizer that performs well at finding local minima.
Particle swarm optimization (PSO) implemented by the pyswarm Python package. This algorithm is computationally expensive but is more robust than ASD in the presence of multiple local-minima.
Bayesian Optimization implemented by the hyperopt Python package. This method balances exploration of global and local minima, and it is designed to work with expensive objective functions. It is less computationally expensive than PSO and is likely to locate the correct local minimum faster than ASD, although after finding it, it is typically slower to converge to the final optimal solution.

The design of the optimization system facilitates its use with general third-party optimization packages, which makes it easy to switch algorithms and compare different depending on their suitability to the specific problem at hand.

Use cases

To illustrate the process of creating a model in the Cascade Analysis Tool, we will construct a hypertension cascade. This cascade is included in the library of demonstration projects available in the Cascade Analysis Tool.

Designing the cascade

To begin, we need to define the structure of the hypertension model. We consider four disease stages – undiagnosed, diagnosed, on treatment, and successfully controlled.

Next, we consider the possible transitions in the model. People begin in the undiagnosed compartment, and then they progress sequentially through the compartments. Once an individual is diagnosed, they cannot lose their diagnosed status, so there is no transition from diagnosed back to undiagnosed. However, an individual on treatment (or with successfully controlled hypertension) may discontinue treatment, so we include a transition from treatment/controlled back to diagnosed to account for this. An individual may die at any stage, so all compartments also have outflows associated with death – typically, the net death rate would be higher for compartments where individuals have untreated hypertension.

Collating data

Data entry in the databook. We construct a hypothetical example loosely based on a study of 28891 adults in Malawi conducted between May 16, 2013, and Feb 8, 2016²², which identified 4096 people with hypertension, of which 1708 were aware of their status, 1183 were receiving treatment, and 440 had controlled blood pressure. We assume these numbers describe the state of the hypertension cascade in 2016 (Figure 4a), and that we want to estimate the state of the cascade in 2017.

Figure 4. (Panel A) Input data on the state of the hypertension cascade; (Panel b) Illustrative hypertension cascade model with flow rates described in blue text; (Panel C) Cascade representation of the hypertension model with the 2016 values as per the input data and the 2017 values derived from applying the flow rates in Panel B.

For flow rates, we assume an incidence rate of 72 per 1000 person-years (averaging the values for reported in 23,24), which gives 255 new cases/year. Next, we set the mortality rate to 18.8/1000, reduced to 13.3/1000 for those with blood pressure control (taken from 25), which implies 75 deaths annually among the study population. Combining these estimates of incidence and mortality implies that the total number of people with hypertension increases by 255-75=180 annually, or 4.4%, consistent with an increasing epidemic. We further assume that the hypertension cascade is in a steady state such that the relative proportions of people in each cascade stage are constant over time, which implies that the number of people in each cascade stage will increase by 4.4% each year. This assumption allows us to solve for flow rates between the hypertension care cascade stages over time and to estimate the number of people in each cascade stage in 2017, depicted in Figure 4. These data and assumptions are then entered into the databook (Figure 5).

Figure 5. Illustration of the data entry book for the hypertension example depicted in Figure 4.

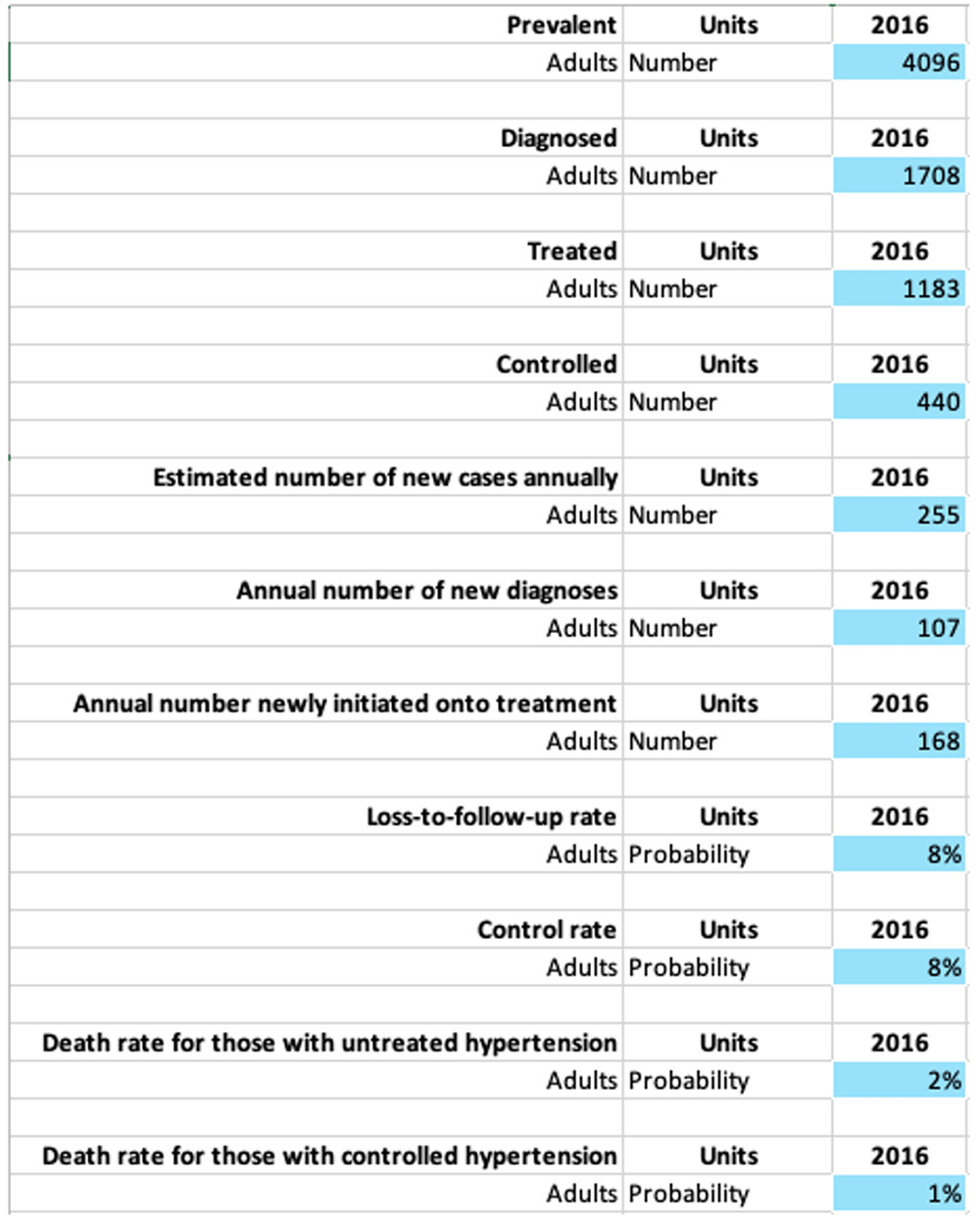
Although we have illustrated values for a single year in this example, the databook supports entering values at multiple time points. Complex models may have many more compartments and parameters, and we have tested the software with highly complex models with ~ 30 compartments and ~150 parameters to verify scalability.

Data entry in the program book. One of the key purposes of a cascade analysis is to understand how various different interventions affect the state of the cascade. In our hypertension cascade example, it would be reasonable to expect that several of the variables that affected the movement of people through the cascade are dependent on interventions that determine the testing, treatment initiation, treatment success, and loss-to follow-up rates.

An essential part of the data collation and curation stage involves assembling a list of the interventions that are likely to have an impact on the cascade. We now illustrate how the programmatic data are used by continuing the hypertension example, supplemented with some assumptions on programmatic data.

We will suppose that people are diagnosed with hypertension after receiving blood pressure tests, and that 2580 such tests were conducted in 2016, either through pharmacies (which we assume provide 55% of tests at a unit cost of $5 and with yield of 3.5%), in clinics (which we assume provide 40% of tests at a unit cost of $20 and with yield of 3.5%), or via an outreach program (which we assume provide the remaining 5% of tests at a unit cost of $15 and with yield of 15%). We suppose that people are initiated onto treatment either immediately after diagnosis (with 20% of those diagnosed at pharmacies, 90% of those diagnosed in clinics, and 70% of those diagnosed via outreach programs being immediately initiated onto treatment), or else people are offered treatment and lifestyle counseling at a unit cost of $25. We also suppose that there is an adherence and lifestyle counseling program to assist those on treatment without blood pressure control (operating at a unit cost of $25 and with 30% of those counseled attaining blood pressure control within 3 months), and retention enhancement initiatives (such as automatic prescription refills, text message reminders for taking medication, or dietary support programs) to counteract loss to follow-up, which increase treatment retention from 88% to 96% at a unit cost per person counseled of $25. Based on what we know about the flow rates through the cascade from Figure 4 and these assumptions about hypothetical programmatic effects, we obtain the programmatic summary documented in Table 1.

Table 1. Illustrative data on interventions for the hypertension example presented in Figure 4.

Intervention	Target cascade stage	Number covered	Unit cost	Baseline investment*	Impact
Pharmacy testing	Undiagnosed	1,430 tested	$5	$7,150	• 50 diagnosed (3.5% yield) • 20% start treatment (10 people)
Clinic testing	Undiagnosed	1,000 tested	$20	$20,000	• 35 diagnosed (3.5% yield) • 90% start treatment (32 people)
Outreach testing	Undiagnosed	150 tested	$15	$2,250	• 22 diagnosed (15% yield) • 70% start treatment (16 people)
Treatment & lifestyle counseling	Diagnosed, not treated	110 counseled	$25	$2,750	• All those counseled start treatment (110 people)
Adherence & lifestyle counseling	Treated, not controlled	200 counseled	$25	$5,000	• 30% of those counseled attain blood pressure control within 3 months (60 people)
Retention enhancement initiatives	All treated	600 covered	$25	$15,000	• 96% treatment retention vs 88% among those not covered (95 people lost)

*Baseline investment is calculated here by multiplying the number of people covered by the unit cost.

Analysis of policy questions

Case scenarios. To illustrate the use of scenarios, we consider six different scenarios in which an additional $10,000 is allocated to each of the six interventions indicated in Table 1 and calculate the impact that this would have on the hypertension cascade introduced in Figure 4. These scenarios are presented in Table 2 and Figure 6.

Table 2. Illustrative scenarios showing different intervention scale-up options, based on the treatment cascade introduced in Figure 3.

Intervention to scale up	Scaled-up budget	Number covered	Impact	Cascade in 2017 (% improvement over baseline)
Pharmacy testing	$17,150	3,430 tested	• 120 diagnosed • 24 start treatment	• Diagnosed: 1853 (4%) • Treated: 1249 (1%) • Controlled: 459 (-)
Clinic testing	$30,000	1,500 tested	• 53 diagnosed • 48 start treatment	• Diagnosed: 1800 (1%) • Treated: 1247 (1%) • Controlled: 459 (-)
Outreach testing	$12,250	817 tested	• 122 diagnosed • 86 start treatment	• Diagnosed: 1883 (6%) • Treated: 1305 (6%) • Controlled: 459 (-)
Treatment & lifestyle counseling	$12,750	510 counseled	• 510 start treatment	• Diagnosed: 1783 (-) • Treated: 1635 (32%) • Controlled: 459 (-)
Adherence & lifestyle counseling	$15,000	600 counseled	• 180 attain control	• Diagnosed: 1783 (-) • Treated: 1235 (-) • Controlled: 579 (26%)
Retention enhancement initiatives	$25,000	1000 covered	• 62 lost to follow-up	• Diagnosed: 1853 (-) • Treated: 1268 (3%) • Controlled: 472 (3%)

Figure 6. The state of the illustrative hypertension cascade in 2017 under the 6 different scale-up options presented in Table 2.

Optimization. The objectives, adjustables, constraints, and optimization algorithms can be flexibly combined by users of the Cascade Analysis Tool. To illustrate the concept of cascade optimization, we return to our hypertension example, where we have an additional $10,000 to improve some cascade outcome. Figure 7 indicates that the best way to spend these additional funds depends on the objective: if we want to maximize the number of people with blood pressure control, the highest priorities are to scale up the adherence & lifestyle counseling program; if we want to maximize the number of people diagnosed, then the outreach testing program is prioritized; and if we want to minimize losses across the whole cascade, the treatment & lifestyle counseling program is prioritized. Here, the adjustment type falls under the heading “immediate one-off allocation change”, since we wish to immediately allocate the additional funds and there are no defined constraints.

Figure 7. Optimal allocations for achieving difference targets related to the illustrative hypertension example.

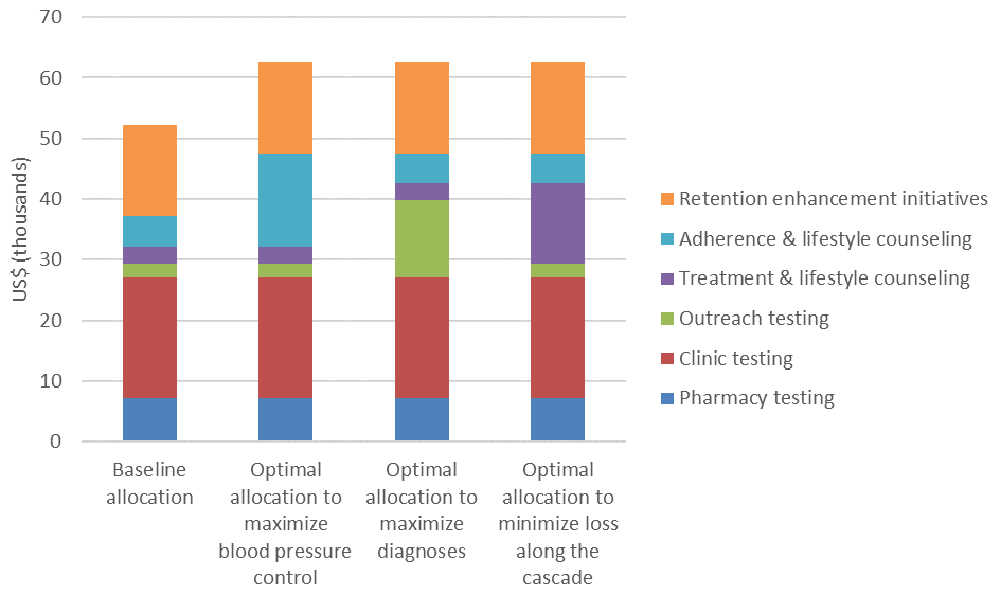
We provide three additional examples of optimization problems:

1. The national government is trying to determine an optimal investment strategy for the HIV response in order to get as close as possible to the target of having 86% of people virally suppressed by 2030 (in line with international targets of having 95% of people with HIV diagnosed, 95% of those diagnosed receiving treatment, and 95% of those treated virally suppressed). The country’s treatment program is currently funded by international donors, who have already announced their investment strategy and will begin gradually defunding the treatment program starting in 2021. The government is committed to providing ongoing care for those already on treatment, so the government’s allocation to the treatment will need to increase to match current levels. In this case:
- a. the objective is to maximize the number of people in the final stage of the cascade;
- b. the adjustment type falls under the heading “ongoing (time-varying) allocation changes”, since the government can change the allocation of funding for the HIV response annually between now and 2030; and,
- c. the constraints are the overall budget in each year, plus the additional constraint that the allocation to the treatment program needs to match current levels after international funders have withdrawn.
2. The national government wants to run a large-scale diabetes screening campaign to get 100,000 people screened within the next year. There are several different service delivery modalities for the screening program (e.g., screening through primary health clinics, workplace programs, community outreach programs, and pharmacies). In this case:
- a. the objective is to minimize the budget required to attain the target of 100,000 people screened;
- b. the adjustment type falls under the heading “immediate one-off allocation change”; and,
- c. there are no defined constraints.
The government is considering a program, to be launched in 2022, to improve the overall cascade of care for pregnant women. In this case:
- a. the objective might be to minimize losses along the cascade;
- b. the adjustment type falls under the heading delayed one-off allocation change”; and,
- c. there may be an overall budget constraint, or other defined constraints such as ensuring minimum funding levels for other programs. For example, it could be specified that funding for the new program can only be taken from new funds plus partial redirection of resources from certain programs while not changing funding for others.

The objectives, adjustables, constraints, and optimization algorithms can be flexibly combined by users of the Cascade Analysis Tool.

Discussion

For complex cascades, it is difficult to determine which programs have the greatest marginal impact. This is especially true when interventions do not target the same populations, do not have the same type of effects, and/or do not have simple linear cost functions. In many cases, the impact of a resource allocation on the cascade may not be known a priori. Moreover, when a large number of interventions are involved, the combinatorial explosion of possible budgets makes it computationally infeasible to explore different possible funding combinations using an undirected approach. Previous studies have already shown that targeting investment to the right combination of effective service delivery modalities across the cascade can lead to greatly improved outcomes^21,26. The Cascade Analysis Tool can help make practical recommendations for how to improve cascade outcomes by making use of the increasing quantities of available raw data on the costs, coverage, and impact of health and development interventions. Given the generality of the approach, there is potential for gains to be identified across any number of application areas.

We have taken several steps to encourage the adoption of our framework for cascade analysis. Firstly, we have implemented the processes for using the generalized framework in an Open Access software package, developed in Python and available via GitHub. Secondly, we have included several simple pre-designed cascades in the software package. Thirdly, we have developed a graphical user interface. A website with additional information and a user guide are also available. Finally, we have run three training workshops (in Bucharest, Bangkok, and Pretoria) as part of the World Bank’s 2018 Skills Building Program (themed “Big Data, Artificial Intelligence and Decision Science in Health and Nutrition”), where we trained approximately 100 users (predominantly representatives from ministries of health, development agencies, and local academic institutions).

Whilst the Cascade Analysis Tool is still in the early stages of existence, we believe there is potential for it to help make sense of the increasing quantities of data on cascades. Furthermore, we hope that the existence of this tool will help motivate the collection of even more data, so that results-based evaluation can continue to guide the decision-making processes in health and development in the future.

Data availability

All data underlying the results are available as part of the article and no additional source data are required.

Software availability

- Software available at: http://ui.cascade.tools/
- Source code available from: https://github.com/atomicateam/atomica
- Archived source code at time of publication: https://doi.org/10.5281/zenodo.3137154²⁷
- License: GNU General Public License v3.0

Grant information

This work was supported by the Bill and Melinda Gates Foundation [OPP1181918].

The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Faculty Opinions recommended

References

1. OECD: The Paris Declaration on Aid Effectiveness. 2005. Reference Source
2. OECD: The Accra Agenda For Action, 3rd High Level Forum on Aid Effectiveness. 2008. Reference Source
3. Biscaye P, LaFayette M, Martin A, et al.: Evaluating Donor-Level Results Measurement Systems. In EPAR Technical report. Evans School of Public Policy and Governance, 2015. Reference Source
4. Piot M: A Simulation model of case finding and treatment in tuberculosis control programmes. In WHO Global Tuberculosis Programme. World Health Organization: Geneva 1967. Reference Source
5. Gardner EM, McLees MP, Steiner JF, et al.: The spectrum of engagement in HIV care and its relevance to test-and-treat strategies for prevention of HIV infection. Clin Infect Dis. 2011; 52(6): 793–800. PubMed Abstract | Publisher Full Text | Free Full Text
6. Kilmarx PH, Mutasa-Apollo T: Patching a leaky pipe: the cascade of HIV care. Curr Opin HIV AIDS. 2013; 8(1): 59–64. PubMed Abstract
7. Gaolathe T, Wirth KE, Holme MP, et al.: Botswana's progress toward achieving the 2020 UNAIDS 90-90-90 antiretroviral therapy and virological suppression goals: a population-based survey. Lancet HIV. 2016; 3(5): e221–e230. PubMed Abstract | Publisher Full Text | Free Full Text
8. UNAIDS: Ending AIDS: progress towards the 90-90-90 targets. Geneva, 2017. Reference Source
9. Stop TB: Global Plan To End TB 2016-2020. 2015. Reference Source
10. Alsdurf H, Hill PC, Matteelli A, et al.: The cascade of care in diagnosis and treatment of latent tuberculosis infection: a systematic review and meta-analysis. Lancet Infect Dis. 2016; 16(11): 1269–1278. PubMed Abstract | Publisher Full Text
11. Naidoo P, Theron G, Rangaka MX, et al.: The South African Tuberculosis Care Cascade: Estimated Losses and Methodological Challenges. J Infect Dis. 2017; 216(suppl_7): S702–s713. PubMed Abstract | Publisher Full Text | Free Full Text
12. Subbaraman R, Nathavitharana RR, Satyanarayana S, et al.: The Tuberculosis Cascade of Care in India's Public Sector: A Systematic Review and Meta-analysis. PLoS Med. 2016; 13(10): e1002149. PubMed Abstract | Publisher Full Text | Free Full Text
13. Ali MK, Bullard KM, Gregg EW, et al.: A cascade of care for diabetes in the United States: visualizing the gaps. Ann Intern Med. 2014; 161(10): 681–689. PubMed Abstract | Publisher Full Text
14. Stokes A, Berry KM, Mchiza Z, et al.: Prevalence and unmet need for diabetes care across the care continuum in a national sample of South African adults: Evidence from the SANHANES-1, 2011-2012. PLoS One. 2017; 12(10): e0184264. PubMed Abstract | Publisher Full Text | Free Full Text
15. Linas BP, Barter DM, Leff JA, et al.: The hepatitis C cascade of care: identifying priorities to improve clinical outcomes. PLoS One. 2014; 9(5): e97317. PubMed Abstract | Publisher Full Text | Free Full Text
16. Murphy RD, Wohl AR, Ma Y, et al.: Adaptation of the HIV Care Continuum as a Method for Evaluating Syphilis and Gonorrhea Disease Control Activities in Los Angeles County. Sex Transm Dis. 2015; 42(12): 686–90. PubMed Abstract | Publisher Full Text
17. Perlman DC, Jordan AE, Nash D: Conceptualizing Care Continua: Lessons from HIV, Hepatitis C Virus, Tuberculosis and Implications for the Development of Improved Care and Prevention Continua. Front Public Health. 2017; 4: 296. PubMed Abstract | Publisher Full Text | Free Full Text
18. Socias ME, Volkow N, Wood E: Adopting the 'cascade of care' framework: an opportunity to close the implementation gap in addiction care? Addiction. 2016; 111(12): 2079–2081. PubMed Abstract | Publisher Full Text | Free Full Text
19. Williams AR, Nunes E, Olfson M: To Battle The Opioid Overdose Epidemic, Deploy The ‘Cascade Of Care’ Model. In Health Affairs Blog. 2017. Reference Source
20. Lessard L, Fournier L, Gauthier J, et al.: Continuum of care for persons with common mental health disorders in Nunavik: a descriptive study. Int J Circumpolar Health. 2015; 74(1): 27186. PubMed Abstract | Publisher Full Text | Free Full Text
21. Olney JJ, Braitstein P, Eaton JW, et al.: Evaluating strategies to improve HIV care outcomes in Kenya: a modelling study. Lancet HIV. 2016; 3(12): e592–e600. PubMed Abstract | Publisher Full Text | Free Full Text
22. Price AJ, Crampin AC, Amberbir A, et al.: Prevalence of obesity, hypertension, and diabetes, and cascade of care in sub-Saharan Africa: a cross-sectional, population-based study in rural and urban Malawi. Lancet Diabetes Endocrinol. 2018; 6(3): 208–222. PubMed Abstract | Publisher Full Text | Free Full Text
23. Hajjar I, Kotchen JM, Kotchen TA: Hypertension: trends in prevalence, incidence, and control. Annu Rev Public Health. 2006; 27(1): 465–490. PubMed Abstract | Publisher Full Text
24. Diez Roux AV, Chambless L, Merkin SS, et al.: Socioeconomic disadvantage and change in blood pressure associated with aging. Circulation. 2002; 106(6): 703–710. PubMed Abstract | Publisher Full Text
25. Ford ES: Trends in mortality from all causes and cardiovascular disease among hypertensive and nonhypertensive adults in the United States. Circulation. 2011; 123(16): 1737–1744. PubMed Abstract | Publisher Full Text
26. McGillen JB, Anderson SJ, Dybul MR, et al.: Optimum resource allocation to reduce HIV incidence across sub-Saharan Africa: a mathematical modelling study. Lancet HIV. 2016; 3(9): e441–8. PubMed Abstract | Publisher Full Text
27. Atomica Team: atomicateam/atomica v1.4.0 (Version v1.4.0). Zenodo. 2019. http://www.doi.org/10.5281/zenodo.3137154

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 07 Jun 2019

Author details Author details

David J Kedziora
Roles: Investigation, Methodology, Software, Writing – Review & Editing

Romesh Abeysuriya
Roles: Investigation, Methodology, Software, Writing – Review & Editing

Cliff C Kerr
Roles: Software, Visualization, Writing – Review & Editing

George L Chadderdon
Roles: Software, Visualization

Vlad-Ștefan Harbuz
Roles: Software, Visualization

Sarah Metzger
Roles: Project Administration, Writing – Review & Editing

David P Wilson
Roles: Conceptualization, Project Administration, Writing – Review & Editing

Robyn M Stuart
Roles: Funding Acquisition, Methodology, Project Administration, Software, Supervision, Writing – Original Draft Preparation, Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

This work was supported by the Bill and Melinda Gates Foundation [OPP1181918].
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Article Versions (2)

version 2

Revised

Published: 24 Dec 2019, 3:1488

https://doi.org/10.12688/gatesopenres.13031.2

version 1

Published: 07 Jun 2019, 3:1488

https://doi.org/10.12688/gatesopenres.13031.1

© 2019 Kedziora DJ et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
Gates Open Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

SEE MORE DETAILS

CITE

how to cite this article

Kedziora DJ, Abeysuriya R, Kerr CC et al. The Cascade Analysis Tool: software to analyze and optimize care cascades [version 1; peer review: 3 approved with reservations]. Gates Open Res 2019, 3:1488 (https://doi.org/10.12688/gatesopenres.13031.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Current Reviewer Status: ?

Key to Reviewer Statuses VIEW HIDE

ApprovedThe paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approvedFundamental flaws in the paper seriously undermine the findings and conclusions

Version 1

VERSION 1

PUBLISHED 07 Jun 2019

Views

Reviewer Report 25 Jul 2019

Mathieu Maheu-Giroux, Department of Epidemiology, Biostatistics, and Occupational Health, McGill University, Montréal, QC, Canada

Approved with Reservations

https://doi.org/10.21956/gatesopenres.14141.r27542

The paper by Kedziora and colleagues present a new software, christened “The Cascade Analysis Tool”, that enables users to optimize resources allocation under budget constraints. The authors provide a generic flexible framework to model different types of cascades, applicable to a wide range of health conditions.

The introduction is well-written and provides a nice background to explain the relevance of the Cascade Analysis Tool. Overall, this is a nice paper that addresses an important issue. However, I found that the methods section is (at time) difficult to read and that some relevant information is missing. These points are further detailed below.

Suggestions:

The authors could consider adding a table or box that would summarize the key data requirements to use this tool. I understand that this can be challenging given that the tool is intended to be generic but it would inform on the key elements required. For example, do we need mortality (or e0) and disease-specific mortality rates? Do we need to have precise estimates on the number (or %) of individuals in each compartment of the cascade?
In the case of infectious diseases where interventions can have externalities, how is onward transmission taken into account? From my understanding of the paper, there is no force of infection specified in the compartmental model. I am not saying that it should absolutely be considered but, at the very least, the assumption of no externalities (i.e., averting chains of transmission) should be made crystal clear in the paper and the implications on budget allocation discussed, including limitations.
It is unclear what are the types of outcomes that can be optimized? From the case studies on the website referred to in the paper (HIV in South Africa; https://cascade.tools/south-africa), it seems that it can be “infection averted” but this is not mentioned in the paper. Where the cascade results plugged in another model (e.g., Optima) to obtain this result?
Also, can QALY or DALY be optimized instead? Based on the sentence “It is possible for users to construct their own objective using any of the model’s outputs, as well as to combine multiple objectives into a single target”, this seems theoretically possible. In any case, I suggest being a little bit more specific about what type of objective functions can, and cannot, be optimized.
For resources allocation, what is the recommended time horizon for the economic evaluation/optimization? I suspect that this is case-specific and must be chosen by the users. I recommend making this clear in the paper. Similar issue with discounting? Can health outcomes and/or budgets be discounted at a user-specified rate? I am not asking that the authors go in details about this… but if these functionalities are readily available (or not) should be mentioned in the relevant section(s).
Also regarding resources allocation, can potential resources savings be considered? For example, earlier management of a chronic condition could save money down the line and this could impact decision-making regarding best allocative strategies.
The paper does an excellent job at explaining which type of questions can be answered with the Cascade Analysis Tool. It would be equally informative if examples of policy questions that cannot be answered (or with difficulty) were presented. For example, the optimization algorithm seems to be agnostic about equity constraints (is that the case)? Can resources allocation among cascades in different geographical regions be performed? Can optimizing two cascades (for different health conditions) that could share some common interventions be achieved?
Figure 5 is confusing as the “LTFU rate”, “Control rate”, and “Death rate” are depicted as unit-less probability. Are these rates (incidence density) or proportions (incidence proportion)?
Can the discussion of the limitations of the model be expanded. For example, what are the implications of the steady state assumption? How much training is needed for public health practitioners to be able to perform analyses on their own with the Cascade Analysis Tool? What set of minimum core competencies are required?

Discretionary revisions

The Methods section has many different types of headers without any clear ordering. Please standardize all headers and sub-headers as the current format is confusing.
Why start the methods with the different packages used (Implementation section)? I am not convinced that this is relevant to your audience.
“Characteristics” is confusing to described quantities that can be derived from the model? Maybe “Indicators” or “Derived metrics” would be more appropriate?
Is it really the “summed loss rates” that are being minimized or the total number of individuals lost at all stages? It seems that these two different ways of conceptualizing losses could give different results.
Why provide a link to the software page if it is password-protected? Will a fee be charged to use it?
Consider renaming the section “Use cases” to “Case studies”.
The GitHub repo refers to “Atomica”. It seems that the latter include more features than the Cascade Analysis Tool, which is slightly confusing. Also, the readme of this repo does not mention the Cascade Analysis Tool. Are “Atomica” and the “Cascade Analysis Tool” the same? If so, could the repo be renamed.

Is the rationale for developing the new software tool clearly explained?

Yes
Is the description of the software tool technically sound?

Yes
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Yes
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Partly
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Partly

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Population health; Infectious disease epidemiology; Mathematical modeling

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

CITE

Report a concern

Author Response 13 Jan 2020

Robyn Stuart, Department of Mathematical Sciences, University of Copenhagen, Universitetsparken 5, Copenhagen, 2100, Denmark

13 Jan 2020

Author Response
We thank the reviewer for taking the time to review, and for providing helpful comments that have greatly strengthened the article. Responses to particular points are provided below.
... Continue reading
We thank the reviewer for taking the time to review, and for providing helpful comments that have greatly strengthened the article. Responses to particular points are provided below.

The paper by Kedziora and colleagues present a new software, christened “The Cascade Analysis Tool”, that enables users to optimize resources allocation under budget constraints. The authors provide a generic flexible framework to model different types of cascades, applicable to a wide range of health conditions. We thank the reviewer for the summary.

The introduction is well-written and provides a nice background to explain the relevance of the Cascade Analysis Tool. Overall, this is a nice paper that addresses an important issue. However, I found that the methods section is (at time) difficult to read and that some relevant information is missing. Thank you, we have reworked the methods section considerably in response to this and other reviewer comments - details are provided below.

The authors could consider adding a table or box that would summarize the key data requirements to use this tool. I understand that this can be challenging given that the tool is intended to be generic but it would inform on the key elements required. For example, do we need mortality (or e0) and disease-specific mortality rates? Do we need to have precise estimates on the number (or %) of individuals in each compartment of the cascade? We have added a summary paragraph on key data requirements to the methods section, as well as a link to the section of the website where this information is summarized.

In the case of infectious diseases where interventions can have externalities, how is onward transmission taken into account? From my understanding of the paper, there is no force of infection specified in the compartmental model. I am not saying that it should absolutely be considered but, at the very least, the assumption of no externalities (i.e., averting chains of transmission) should be made crystal clear in the paper and the implications on budget allocation discussed, including limitations. Atomica, the model that powers the Cascade Analysis Tool, can be used to set up arbitrary compartmental models, including models with a force of infection and onward transmission. This functionality is carried over to the Cascade Analysis Tool, but it’s not the main intended use case of the tool. We have tried to clarify this in the discussion section.

It is unclear what are the types of outcomes that can be optimized? From the case studies on the website referred to in the paper (HIV in South Africa; https://cascade.tools/south-africa), it seems that it can be “infection averted” but this is not mentioned in the paper. Where the cascade results plugged in another model (e.g., Optima) to obtain this result? We have added text to the limitations paragraph of the discussion section on this: “the web application was designed specifically for supporting cascade analyses, but the underlying model (Atomica) has additional functionalities that have not been introduced to the web application. For example, with Atomica one can specify a much broader range of optimization objectives (e.g. minimizing new infections, disease-related deaths, or DALYs), whereas the Cascade Analysis Tool web application only supports cascade-related objectives. Therefore, whilst it is possible to specify any compartmental model in the Cascade Analysis Tool (e.g. an SIR model with onward transmission), the set of analyses that can be conducted in the web application are limited to the cascade-related ones described in this paper.”

Also, can QALY or DALY be optimized instead? Based on the sentence “It is possible for users to construct their own objective using any of the model’s outputs, as well as to combine multiple objectives into a single target”, this seems theoretically possible. In any case, I suggest being a little bit more specific about what type of objective functions can, and cannot, be optimized. Yes, see above.

For resources allocation, what is the recommended time horizon for the economic evaluation/optimization? I suspect that this is case-specific and must be chosen by the users. I recommend making this clear in the paper. Similar issue with discounting? Can health outcomes and/or budgets be discounted at a user-specified rate? I am not asking that the authors go in details about this… but if these functionalities are readily available (or not) should be mentioned in the relevant section(s). Indeed, this is all to be specified by the user. Discounting is not currently supported, and we have added a note on this to the limitations section.

Also regarding resources allocation, can potential resources savings be considered? For example, earlier management of a chronic condition could save money down the line and this could impact decision-making regarding best allocative strategies. This is not possible, we’ve added this to the limitations.

The paper does an excellent job at explaining which type of questions can be answered with the Cascade Analysis Tool. It would be equally informative if examples of policy questions that cannot be answered (or with difficulty) were presented. For example, the optimization algorithm seems to be agnostic about equity constraints (is that the case)? Can resources allocation among cascades in different geographical regions be performed? Can optimizing two cascades (for different health conditions) that could share some common interventions be achieved? We’ve added some text addressing this point to the discussion section: “We are also working on extensions to the underlying model to support new types of policy questions, including questions around equity (e.g., which interventions should be prioritized to maximize equity of access to interventions like vaccines), geographical prioritization, and interrelated diseases (e.g., prioritization of integrated services for HIV/TB).”

Figure 5 is confusing as the “LTFU rate”, “Control rate”, and “Death rate” are depicted as unit-less probability. Are these rates (incidence density) or proportions (incidence proportion)? We have addressed this (also noted by reviewer 1).

Can the discussion of the limitations of the model be expanded. For example, what are the implications of the steady state assumption? How much training is needed for public health practitioners to be able to perform analyses on their own with the Cascade Analysis Tool? What set of minimum core competencies are required? We have significantly expanded the section on limitations and addressed these points.

The Methods section has many different types of headers without any clear ordering. Please standardize all headers and sub-headers as the current format is confusing.We have rearranged this section (also in response to comments from the other two reviewers). Why start the methods with the different packages used (Implementation section)? I am not convinced that this is relevant to your audience. According to the journal submission guidelines, this type of article needs to include subsections on Implementation (describing how the tool works and any relevant technical details required for implementation) and Operation (including the minimal system requirements needed to run the software and an overview of the workflow). This subsection on which packages were used was added as per an editor request.

“Characteristics” is confusing to described quantities that can be derived from the model? Maybe “Indicators” or “Derived metrics” would be more appropriate? We agree with this suggestion and have removed the word “characteristics”.

Is it really the “summed loss rates” that are being minimized or the total number of individuals lost at all stages? It seems that these two different ways of conceptualizing losses could give different results. We have changed to: “Minimize the total number of people lost from each stage of the cascade”.

Why provide a link to the software page if it is password-protected? Will a fee be charged to use it? The software requires users to log in, but it is free to create an account. New users can register by clicking “Register here” at http://ui.cascade.tools/

Consider renaming the section “Use cases” to “Case studies”.“Use cases” is suggested by the article submission guidelines.

The GitHub repo refers to “Atomica”. It seems that the latter include more features than the Cascade Analysis Tool, which is slightly confusing. Also, the readme of this repo does not mention the Cascade Analysis Tool. Are “Atomica” and the “Cascade Analysis Tool” the same? If so, could the repo be renamed. We agree it was confusing and have clarified in the text.
We thank the reviewer for taking the time to review, and for providing helpful comments that have greatly strengthened the article. Responses to particular points are provided below.

The paper by Kedziora and colleagues present a new software, christened “The Cascade Analysis Tool”, that enables users to optimize resources allocation under budget constraints. The authors provide a generic flexible framework to model different types of cascades, applicable to a wide range of health conditions. We thank the reviewer for the summary.

The introduction is well-written and provides a nice background to explain the relevance of the Cascade Analysis Tool. Overall, this is a nice paper that addresses an important issue. However, I found that the methods section is (at time) difficult to read and that some relevant information is missing. Thank you, we have reworked the methods section considerably in response to this and other reviewer comments - details are provided below.

The authors could consider adding a table or box that would summarize the key data requirements to use this tool. I understand that this can be challenging given that the tool is intended to be generic but it would inform on the key elements required. For example, do we need mortality (or e0) and disease-specific mortality rates? Do we need to have precise estimates on the number (or %) of individuals in each compartment of the cascade? We have added a summary paragraph on key data requirements to the methods section, as well as a link to the section of the website where this information is summarized.

In the case of infectious diseases where interventions can have externalities, how is onward transmission taken into account? From my understanding of the paper, there is no force of infection specified in the compartmental model. I am not saying that it should absolutely be considered but, at the very least, the assumption of no externalities (i.e., averting chains of transmission) should be made crystal clear in the paper and the implications on budget allocation discussed, including limitations. Atomica, the model that powers the Cascade Analysis Tool, can be used to set up arbitrary compartmental models, including models with a force of infection and onward transmission. This functionality is carried over to the Cascade Analysis Tool, but it’s not the main intended use case of the tool. We have tried to clarify this in the discussion section.

It is unclear what are the types of outcomes that can be optimized? From the case studies on the website referred to in the paper (HIV in South Africa; https://cascade.tools/south-africa), it seems that it can be “infection averted” but this is not mentioned in the paper. Where the cascade results plugged in another model (e.g., Optima) to obtain this result? We have added text to the limitations paragraph of the discussion section on this: “the web application was designed specifically for supporting cascade analyses, but the underlying model (Atomica) has additional functionalities that have not been introduced to the web application. For example, with Atomica one can specify a much broader range of optimization objectives (e.g. minimizing new infections, disease-related deaths, or DALYs), whereas the Cascade Analysis Tool web application only supports cascade-related objectives. Therefore, whilst it is possible to specify any compartmental model in the Cascade Analysis Tool (e.g. an SIR model with onward transmission), the set of analyses that can be conducted in the web application are limited to the cascade-related ones described in this paper.”

Also, can QALY or DALY be optimized instead? Based on the sentence “It is possible for users to construct their own objective using any of the model’s outputs, as well as to combine multiple objectives into a single target”, this seems theoretically possible. In any case, I suggest being a little bit more specific about what type of objective functions can, and cannot, be optimized. Yes, see above.

For resources allocation, what is the recommended time horizon for the economic evaluation/optimization? I suspect that this is case-specific and must be chosen by the users. I recommend making this clear in the paper. Similar issue with discounting? Can health outcomes and/or budgets be discounted at a user-specified rate? I am not asking that the authors go in details about this… but if these functionalities are readily available (or not) should be mentioned in the relevant section(s). Indeed, this is all to be specified by the user. Discounting is not currently supported, and we have added a note on this to the limitations section.

Also regarding resources allocation, can potential resources savings be considered? For example, earlier management of a chronic condition could save money down the line and this could impact decision-making regarding best allocative strategies. This is not possible, we’ve added this to the limitations.

The paper does an excellent job at explaining which type of questions can be answered with the Cascade Analysis Tool. It would be equally informative if examples of policy questions that cannot be answered (or with difficulty) were presented. For example, the optimization algorithm seems to be agnostic about equity constraints (is that the case)? Can resources allocation among cascades in different geographical regions be performed? Can optimizing two cascades (for different health conditions) that could share some common interventions be achieved? We’ve added some text addressing this point to the discussion section: “We are also working on extensions to the underlying model to support new types of policy questions, including questions around equity (e.g., which interventions should be prioritized to maximize equity of access to interventions like vaccines), geographical prioritization, and interrelated diseases (e.g., prioritization of integrated services for HIV/TB).”

Figure 5 is confusing as the “LTFU rate”, “Control rate”, and “Death rate” are depicted as unit-less probability. Are these rates (incidence density) or proportions (incidence proportion)? We have addressed this (also noted by reviewer 1).

Can the discussion of the limitations of the model be expanded. For example, what are the implications of the steady state assumption? How much training is needed for public health practitioners to be able to perform analyses on their own with the Cascade Analysis Tool? What set of minimum core competencies are required? We have significantly expanded the section on limitations and addressed these points.

The Methods section has many different types of headers without any clear ordering. Please standardize all headers and sub-headers as the current format is confusing.We have rearranged this section (also in response to comments from the other two reviewers). Why start the methods with the different packages used (Implementation section)? I am not convinced that this is relevant to your audience. According to the journal submission guidelines, this type of article needs to include subsections on Implementation (describing how the tool works and any relevant technical details required for implementation) and Operation (including the minimal system requirements needed to run the software and an overview of the workflow). This subsection on which packages were used was added as per an editor request.

“Characteristics” is confusing to described quantities that can be derived from the model? Maybe “Indicators” or “Derived metrics” would be more appropriate? We agree with this suggestion and have removed the word “characteristics”.

Is it really the “summed loss rates” that are being minimized or the total number of individuals lost at all stages? It seems that these two different ways of conceptualizing losses could give different results. We have changed to: “Minimize the total number of people lost from each stage of the cascade”.

Why provide a link to the software page if it is password-protected? Will a fee be charged to use it? The software requires users to log in, but it is free to create an account. New users can register by clicking “Register here” at http://ui.cascade.tools/

Consider renaming the section “Use cases” to “Case studies”.“Use cases” is suggested by the article submission guidelines.

The GitHub repo refers to “Atomica”. It seems that the latter include more features than the Cascade Analysis Tool, which is slightly confusing. Also, the readme of this repo does not mention the Cascade Analysis Tool. Are “Atomica” and the “Cascade Analysis Tool” the same? If so, could the repo be renamed. We agree it was confusing and have clarified in the text.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 13 Jan 2020

Robyn Stuart, Department of Mathematical Sciences, University of Copenhagen, Universitetsparken 5, Copenhagen, 2100, Denmark

13 Jan 2020

Author Response
We thank the reviewer for taking the time to review, and for providing helpful comments that have greatly strengthened the article. Responses to particular points are provided below.
... Continue reading
We thank the reviewer for taking the time to review, and for providing helpful comments that have greatly strengthened the article. Responses to particular points are provided below.

The paper by Kedziora and colleagues present a new software, christened “The Cascade Analysis Tool”, that enables users to optimize resources allocation under budget constraints. The authors provide a generic flexible framework to model different types of cascades, applicable to a wide range of health conditions. We thank the reviewer for the summary.

The introduction is well-written and provides a nice background to explain the relevance of the Cascade Analysis Tool. Overall, this is a nice paper that addresses an important issue. However, I found that the methods section is (at time) difficult to read and that some relevant information is missing. Thank you, we have reworked the methods section considerably in response to this and other reviewer comments - details are provided below.

The authors could consider adding a table or box that would summarize the key data requirements to use this tool. I understand that this can be challenging given that the tool is intended to be generic but it would inform on the key elements required. For example, do we need mortality (or e0) and disease-specific mortality rates? Do we need to have precise estimates on the number (or %) of individuals in each compartment of the cascade? We have added a summary paragraph on key data requirements to the methods section, as well as a link to the section of the website where this information is summarized.

In the case of infectious diseases where interventions can have externalities, how is onward transmission taken into account? From my understanding of the paper, there is no force of infection specified in the compartmental model. I am not saying that it should absolutely be considered but, at the very least, the assumption of no externalities (i.e., averting chains of transmission) should be made crystal clear in the paper and the implications on budget allocation discussed, including limitations. Atomica, the model that powers the Cascade Analysis Tool, can be used to set up arbitrary compartmental models, including models with a force of infection and onward transmission. This functionality is carried over to the Cascade Analysis Tool, but it’s not the main intended use case of the tool. We have tried to clarify this in the discussion section.

It is unclear what are the types of outcomes that can be optimized? From the case studies on the website referred to in the paper (HIV in South Africa; https://cascade.tools/south-africa), it seems that it can be “infection averted” but this is not mentioned in the paper. Where the cascade results plugged in another model (e.g., Optima) to obtain this result? We have added text to the limitations paragraph of the discussion section on this: “the web application was designed specifically for supporting cascade analyses, but the underlying model (Atomica) has additional functionalities that have not been introduced to the web application. For example, with Atomica one can specify a much broader range of optimization objectives (e.g. minimizing new infections, disease-related deaths, or DALYs), whereas the Cascade Analysis Tool web application only supports cascade-related objectives. Therefore, whilst it is possible to specify any compartmental model in the Cascade Analysis Tool (e.g. an SIR model with onward transmission), the set of analyses that can be conducted in the web application are limited to the cascade-related ones described in this paper.”

Also, can QALY or DALY be optimized instead? Based on the sentence “It is possible for users to construct their own objective using any of the model’s outputs, as well as to combine multiple objectives into a single target”, this seems theoretically possible. In any case, I suggest being a little bit more specific about what type of objective functions can, and cannot, be optimized. Yes, see above.

For resources allocation, what is the recommended time horizon for the economic evaluation/optimization? I suspect that this is case-specific and must be chosen by the users. I recommend making this clear in the paper. Similar issue with discounting? Can health outcomes and/or budgets be discounted at a user-specified rate? I am not asking that the authors go in details about this… but if these functionalities are readily available (or not) should be mentioned in the relevant section(s). Indeed, this is all to be specified by the user. Discounting is not currently supported, and we have added a note on this to the limitations section.

Also regarding resources allocation, can potential resources savings be considered? For example, earlier management of a chronic condition could save money down the line and this could impact decision-making regarding best allocative strategies. This is not possible, we’ve added this to the limitations.

The paper does an excellent job at explaining which type of questions can be answered with the Cascade Analysis Tool. It would be equally informative if examples of policy questions that cannot be answered (or with difficulty) were presented. For example, the optimization algorithm seems to be agnostic about equity constraints (is that the case)? Can resources allocation among cascades in different geographical regions be performed? Can optimizing two cascades (for different health conditions) that could share some common interventions be achieved? We’ve added some text addressing this point to the discussion section: “We are also working on extensions to the underlying model to support new types of policy questions, including questions around equity (e.g., which interventions should be prioritized to maximize equity of access to interventions like vaccines), geographical prioritization, and interrelated diseases (e.g., prioritization of integrated services for HIV/TB).”

Figure 5 is confusing as the “LTFU rate”, “Control rate”, and “Death rate” are depicted as unit-less probability. Are these rates (incidence density) or proportions (incidence proportion)? We have addressed this (also noted by reviewer 1).

Can the discussion of the limitations of the model be expanded. For example, what are the implications of the steady state assumption? How much training is needed for public health practitioners to be able to perform analyses on their own with the Cascade Analysis Tool? What set of minimum core competencies are required? We have significantly expanded the section on limitations and addressed these points.

The Methods section has many different types of headers without any clear ordering. Please standardize all headers and sub-headers as the current format is confusing.We have rearranged this section (also in response to comments from the other two reviewers). Why start the methods with the different packages used (Implementation section)? I am not convinced that this is relevant to your audience. According to the journal submission guidelines, this type of article needs to include subsections on Implementation (describing how the tool works and any relevant technical details required for implementation) and Operation (including the minimal system requirements needed to run the software and an overview of the workflow). This subsection on which packages were used was added as per an editor request.

“Characteristics” is confusing to described quantities that can be derived from the model? Maybe “Indicators” or “Derived metrics” would be more appropriate? We agree with this suggestion and have removed the word “characteristics”.

Is it really the “summed loss rates” that are being minimized or the total number of individuals lost at all stages? It seems that these two different ways of conceptualizing losses could give different results. We have changed to: “Minimize the total number of people lost from each stage of the cascade”.

Why provide a link to the software page if it is password-protected? Will a fee be charged to use it? The software requires users to log in, but it is free to create an account. New users can register by clicking “Register here” at http://ui.cascade.tools/

Consider renaming the section “Use cases” to “Case studies”.“Use cases” is suggested by the article submission guidelines.

The GitHub repo refers to “Atomica”. It seems that the latter include more features than the Cascade Analysis Tool, which is slightly confusing. Also, the readme of this repo does not mention the Cascade Analysis Tool. Are “Atomica” and the “Cascade Analysis Tool” the same? If so, could the repo be renamed. We agree it was confusing and have clarified in the text.
We thank the reviewer for taking the time to review, and for providing helpful comments that have greatly strengthened the article. Responses to particular points are provided below.

The paper by Kedziora and colleagues present a new software, christened “The Cascade Analysis Tool”, that enables users to optimize resources allocation under budget constraints. The authors provide a generic flexible framework to model different types of cascades, applicable to a wide range of health conditions. We thank the reviewer for the summary.

The introduction is well-written and provides a nice background to explain the relevance of the Cascade Analysis Tool. Overall, this is a nice paper that addresses an important issue. However, I found that the methods section is (at time) difficult to read and that some relevant information is missing. Thank you, we have reworked the methods section considerably in response to this and other reviewer comments - details are provided below.

The authors could consider adding a table or box that would summarize the key data requirements to use this tool. I understand that this can be challenging given that the tool is intended to be generic but it would inform on the key elements required. For example, do we need mortality (or e0) and disease-specific mortality rates? Do we need to have precise estimates on the number (or %) of individuals in each compartment of the cascade? We have added a summary paragraph on key data requirements to the methods section, as well as a link to the section of the website where this information is summarized.

In the case of infectious diseases where interventions can have externalities, how is onward transmission taken into account? From my understanding of the paper, there is no force of infection specified in the compartmental model. I am not saying that it should absolutely be considered but, at the very least, the assumption of no externalities (i.e., averting chains of transmission) should be made crystal clear in the paper and the implications on budget allocation discussed, including limitations. Atomica, the model that powers the Cascade Analysis Tool, can be used to set up arbitrary compartmental models, including models with a force of infection and onward transmission. This functionality is carried over to the Cascade Analysis Tool, but it’s not the main intended use case of the tool. We have tried to clarify this in the discussion section.

It is unclear what are the types of outcomes that can be optimized? From the case studies on the website referred to in the paper (HIV in South Africa; https://cascade.tools/south-africa), it seems that it can be “infection averted” but this is not mentioned in the paper. Where the cascade results plugged in another model (e.g., Optima) to obtain this result? We have added text to the limitations paragraph of the discussion section on this: “the web application was designed specifically for supporting cascade analyses, but the underlying model (Atomica) has additional functionalities that have not been introduced to the web application. For example, with Atomica one can specify a much broader range of optimization objectives (e.g. minimizing new infections, disease-related deaths, or DALYs), whereas the Cascade Analysis Tool web application only supports cascade-related objectives. Therefore, whilst it is possible to specify any compartmental model in the Cascade Analysis Tool (e.g. an SIR model with onward transmission), the set of analyses that can be conducted in the web application are limited to the cascade-related ones described in this paper.”

Also, can QALY or DALY be optimized instead? Based on the sentence “It is possible for users to construct their own objective using any of the model’s outputs, as well as to combine multiple objectives into a single target”, this seems theoretically possible. In any case, I suggest being a little bit more specific about what type of objective functions can, and cannot, be optimized. Yes, see above.

For resources allocation, what is the recommended time horizon for the economic evaluation/optimization? I suspect that this is case-specific and must be chosen by the users. I recommend making this clear in the paper. Similar issue with discounting? Can health outcomes and/or budgets be discounted at a user-specified rate? I am not asking that the authors go in details about this… but if these functionalities are readily available (or not) should be mentioned in the relevant section(s). Indeed, this is all to be specified by the user. Discounting is not currently supported, and we have added a note on this to the limitations section.

Also regarding resources allocation, can potential resources savings be considered? For example, earlier management of a chronic condition could save money down the line and this could impact decision-making regarding best allocative strategies. This is not possible, we’ve added this to the limitations.

The paper does an excellent job at explaining which type of questions can be answered with the Cascade Analysis Tool. It would be equally informative if examples of policy questions that cannot be answered (or with difficulty) were presented. For example, the optimization algorithm seems to be agnostic about equity constraints (is that the case)? Can resources allocation among cascades in different geographical regions be performed? Can optimizing two cascades (for different health conditions) that could share some common interventions be achieved? We’ve added some text addressing this point to the discussion section: “We are also working on extensions to the underlying model to support new types of policy questions, including questions around equity (e.g., which interventions should be prioritized to maximize equity of access to interventions like vaccines), geographical prioritization, and interrelated diseases (e.g., prioritization of integrated services for HIV/TB).”

Figure 5 is confusing as the “LTFU rate”, “Control rate”, and “Death rate” are depicted as unit-less probability. Are these rates (incidence density) or proportions (incidence proportion)? We have addressed this (also noted by reviewer 1).

Can the discussion of the limitations of the model be expanded. For example, what are the implications of the steady state assumption? How much training is needed for public health practitioners to be able to perform analyses on their own with the Cascade Analysis Tool? What set of minimum core competencies are required? We have significantly expanded the section on limitations and addressed these points.

The Methods section has many different types of headers without any clear ordering. Please standardize all headers and sub-headers as the current format is confusing.We have rearranged this section (also in response to comments from the other two reviewers). Why start the methods with the different packages used (Implementation section)? I am not convinced that this is relevant to your audience. According to the journal submission guidelines, this type of article needs to include subsections on Implementation (describing how the tool works and any relevant technical details required for implementation) and Operation (including the minimal system requirements needed to run the software and an overview of the workflow). This subsection on which packages were used was added as per an editor request.

“Characteristics” is confusing to described quantities that can be derived from the model? Maybe “Indicators” or “Derived metrics” would be more appropriate? We agree with this suggestion and have removed the word “characteristics”.

Is it really the “summed loss rates” that are being minimized or the total number of individuals lost at all stages? It seems that these two different ways of conceptualizing losses could give different results. We have changed to: “Minimize the total number of people lost from each stage of the cascade”.

Why provide a link to the software page if it is password-protected? Will a fee be charged to use it? The software requires users to log in, but it is free to create an account. New users can register by clicking “Register here” at http://ui.cascade.tools/

Consider renaming the section “Use cases” to “Case studies”.“Use cases” is suggested by the article submission guidelines.

The GitHub repo refers to “Atomica”. It seems that the latter include more features than the Cascade Analysis Tool, which is slightly confusing. Also, the readme of this repo does not mention the Cascade Analysis Tool. Are “Atomica” and the “Cascade Analysis Tool” the same? If so, could the repo be renamed. We agree it was confusing and have clarified in the text.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Views

Reviewer Report 22 Jul 2019

Ramnath Subbaraman, Department of Public Health and Community Medicine, Tufts University School of Medicine, Boston, MA, USA

Approved with Reservations

https://doi.org/10.21956/gatesopenres.14141.r27363

This is a very thoughtfully written article on a potentially helpful software tool. The goal of the tool is:

To facilitate the construction of care cascades for different diseases, including a flexible platform for developing such

This is a very thoughtfully written article on a potentially helpful software tool. The goal of the tool is:

To facilitate the construction of care cascades for different diseases, including a flexible platform for developing such care cascades that recognizes that each disease will have different steps/stages required and different approaches to patient transitions between stages.
Facilitate construction of care cascade by specific sub-populations (e.g., gender, presumably age, etc.)
To allow estimation of the impact of interventions to improve outcomes in disease-specific care cascades.

Overall, the manuscript is very well-written and communicates key points in sufficient detail. More sophisticated critiques would emerge only, I think, as more people practically use this software for programmatic purposes.

I have the following major and minor points of feedback:

Major Feedback:

Ideally, there would be some platform for public comment, critique, and feedback on this software platform as users engage with it. One of the challenges with reviewing this manuscript is that, while I spent a bit of time playing with the software, it is challenging to provide specific feedback on its strengths or deficiencies without actually using it in practice for a specific disease and programmatic analysis. As such, I think ongoing public feedback on the software from actual users is more critical than peer review of this manuscript.
Care cascades for different diseases deal with transitions differently. For example, most HIV care cascades look at transitions backwards as well as forwards across stages (or "compartments"). In contrast, in most care cascades for active TB, patients can only move forward across care cascade stages, and they can have multiple types of poor outcomes in each "gap" (i.e., difference between steps / stages / compartments). For example, for patients who start treatment but do not complete TB treatment, they could have one of 3 poor outcomes: (a) death, (b) treatment failure, and (c) loss to follow-up. The assumption is that "loss to follow-up" patients do not move "backwards" in the care cascade but fall out completely (and would have to restart from the beginning). Two questions related to this: (a) can this software modeling approach manage care cascades that only have transitions in the forward direction (I am assuming yes from Fig 3, but would be helpful to clarify); and (b) can this software modeling approach capture and estimate different types of poor outcomes as described above?

Clarifying both of these questions in the text would be helpful for readers coming from different disease backgrounds and envisioning the approach differently.

A key point in the manuscript is this statement: "In many real-world situations, the impact of changing intervention coverage and the way interventions should be prioritized is not clear from the analysis of intervention properties alone." This is an important point that may not be evident to readers who don't frequently look at modeling data that look at broader implications and impacts of interventions. When I read this, I had a few thoughts regarding how the authors could expand on this point:

It would be helpful for the authors to add a few sentences explaining this point further. If we already have data on a particular intervention and its impact on reducing a given gap in care, what are the additional benefits of the type of modeling proposed by the authors?
One practical problem that users of this software will face may be the lack of available data on the effect sizes and costing of different interventions to reduce gaps in care. It would be helpful for the authors to specify what types of data / findings users of the software should have available to use this tool. Do they need effect sizes of an intervention to reduce a gap in the care cascade (i.e., estimated % reduction in a poor outcome at a particular step from an intervention)? Do they need confidence intervals for this effect estimate? Do they need these effect size estimates for an intervention for multiple care cascade steps (if an intervention improves outcomes at multiple steps)? What kind of costing data do they need to use this tool?

Finally, it would be helpful for the authors to provide some real world examples of the types of studies that are available from which users of the software can provide these estimates. Even providing citations, example effect sizes or costing data from the existing literature for studies from HIV (for example, since they are most broadly available here) would help readers to think about the types of data they can seek out for their own diseases to populate these models.

Minor Comments:

Authors might consider including a citation for the Lancet Global Health Commission on High-Quality Health Systems, as that major report has argued for care cascade analyses as being a central component of health quality dashboards for understanding quality of care. This strengthens the argument for a user friendly tool such as the one created by these authors.
In paragraph 2 of the paper, the authors should also note that the phrase "continuum of care" has also been used for these types of analyses. This is now emerging as the predominant language for these analyses in HIV, with the assumption that patients can move backwards as well as forwards along this continuum of care.
Paragraph 3 of the Introduction: The authors can correct the way they have described the TB care cascade analyses. The India and South Africa care cascades that have been cited for TB look at active TB disease, while the latent TB care cascade cited looks at latent TB disease. As such, these are two different frameworks for different types of TB--i.e., it is not that the framework in citation 10 guides the framework in citations 11 and 12--they are different frameworks for different forms of TB. A more detailed methods framework for active TB disease is available in the manuscript: Subbaraman R, Nathavitharana RR, Mayer KH, Satyanarayana S, Chadha VK, Arinaminpathy N, et al. (2019) Constructing care cascades for active tuberculosis: A strategy for program monitoring and identifying gaps in quality of care¹. Such methodological manuscripts could inform development of models using a tool such as the one the authors have created.

Is the rationale for developing the new software tool clearly explained?

Yes
Is the description of the software tool technically sound?

Yes
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Yes
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Yes
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Yes

References

1. Subbaraman R, Nathavitharana RR, Mayer KH, Satyanarayana S, et al.: Constructing care cascades for active tuberculosis: A strategy for program monitoring and identifying gaps in quality of care.PLoS Med. 2019; 16 (2): e1002754 PubMed Abstract | Publisher Full Text

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: tuberculosis implementation science, infectious diseases epidemiology

CITE

Report a concern

Author Response 13 Jan 2020

Robyn Stuart, Department of Mathematical Sciences, University of Copenhagen, Universitetsparken 5, Copenhagen, 2100, Denmark

13 Jan 2020

Author Response
- Ideally, there would be some platform for public comment, critique, and feedback on this software platform as users engage with it. One of the challenges with reviewing this
... Continue reading
Ideally, there would be some platform for public comment, critique, and feedback on this software platform as users engage with it. One of the challenges with reviewing this manuscript is that, while I spent a bit of time playing with the software, it is challenging to provide specific feedback on its strengths or deficiencies without actually using it in practice for a specific disease and programmatic analysis. As such, I think ongoing public feedback on the software from actual users is more critical than peer review of this manuscript. We thank the reviewer for this excellent suggestion. We have added a blog to our website (where we can also post information on updates to the tool). Users can provide feedback via the comments section.

Care cascades for different diseases deal with transitions differently. For example, most HIV care cascades look at transitions backwards as well as forwards across stages (or "compartments"). In contrast, in most care cascades for active TB, patients can only move forward across care cascade stages, and they can have multiple types of poor outcomes in each "gap" (i.e., difference between steps / stages / compartments). For example, for patients who start treatment but do not complete TB treatment, they could have one of 3 poor outcomes: (a) death, (b) treatment failure, and (c) loss to follow-up. The assumption is that "loss to follow-up" patients do not move "backwards" in the care cascade but fall out completely (and would have to restart from the beginning). Two questions related to this: (a) can this software modeling approach manage care cascades that only have transitions in the forward direction (I am assuming yes from Fig 3, but would be helpful to clarify); and (b) can this software modeling approach capture and estimate different types of poor outcomes as described above? Clarifying both of these questions in the text would be helpful for readers coming from different disease backgrounds and envisioning the approach differently. Yes, both types of cascade can be modelled with the tool. We have added text on this to the methods section.

A key point in the manuscript is this statement: "In many real-world situations, the impact of changing intervention coverage and the way interventions should be prioritized is not clear from the analysis of intervention properties alone." This is an important point that may not be evident to readers who don't frequently look at modeling data that look at broader implications and impacts of interventions. When I read this, I had a few thoughts regarding how the authors could expand on this point:

It would be helpful for the authors to add a few sentences explaining this point further. If we already have data on a particular intervention and its impact on reducing a given gap in care, what are the additional benefits of the type of modeling proposed by the authors?

One practical problem that users of this software will face may be the lack of available data on the effect sizes and costing of different interventions to reduce gaps in care. It would be helpful for the authors to specify what types of data / findings users of the software should have available to use this tool. Do they need effect sizes of an intervention to reduce a gap in the care cascade (i.e., estimated % reduction in a poor outcome at a particular step from an intervention)? Do they need confidence intervals for this effect estimate? Do they need these effect size estimates for an intervention for multiple care cascade steps (if an intervention improves outcomes at multiple steps)? What kind of costing data do they need to use this tool?

Finally, it would be helpful for the authors to provide some real world examples of the types of studies that are available from which users of the software can provide these estimates. Even providing citations, example effect sizes or costing data from the existing literature for studies from HIV (for example, since they are most broadly available here) would help readers to think about the types of data they can seek out for their own diseases to populate these models.

We have:

Moved this text to a more prominent position in the article, and emphasized it more clearly by repeating it in the discussion section as well.

“One practical problem that users of this software will face may be the lack of available data on the effect sizes and costing of different interventions to reduce gaps in care.” -- we added a section noting the issues related to data availability in the methods.

“It would be helpful for the authors to specify what types of data / findings users of the software should have available to use this tool.” - we added a section on minimum data requirements to the data entry section of the methods

“Do they need effect sizes of an intervention to reduce a gap in the care cascade (i.e., estimated % reduction in a poor outcome at a particular step from an intervention)” -- yes, this is needed, and we’ve added text clarifying this.

“Do they need confidence intervals for this effect estimate?” -- this is not required.

“Do they need these effect size estimates for an intervention for multiple care cascade steps (if an intervention improves outcomes at multiple steps)? What kind of costing data do they need to use this tool?” - we have specified this in the data entry section.

We have added a paragraph on typical data sources.

Authors might consider including a citation for the Lancet Global Health Commission on High-Quality Health Systems, as that major report has argued for care cascade analyses as being a central component of health quality dashboards for understanding quality of care. This strengthens the argument for a user friendly tool such as the one created by these authors. Thank you, we have added this.

In paragraph 2 of the paper, the authors should also note that the phrase "continuum of care" has also been used for these types of analyses. This is now emerging as the predominant language for these analyses in HIV, with the assumption that patients can move backwards as well as forwards along this continuum of care. Thank you, we have added this.

Paragraph 3 of the Introduction: The authors can correct the way they have described the TB care cascade analyses. The India and South Africa care cascades that have been cited for TB look at active TB disease, while the latent TB care cascade cited looks at latent TB disease. As such, these are two different frameworks for different types of TB--i.e., it is not that the framework in citation 10 guides the framework in citations 11 and 12--they are different frameworks for different forms of TB. A more detailed methods framework for active TB disease is available in the manuscript: Subbaraman R, Nathavitharana RR, Mayer KH, Satyanarayana S, Chadha VK, Arinaminpathy N, et al. (2019) Constructing care cascades for active tuberculosis: A strategy for program monitoring and identifying gaps in quality of care1. Such methodological manuscripts could inform development of models using a tool such as the one the authors have created. Thank you, we have fixed this and added the suggested citation.
Ideally, there would be some platform for public comment, critique, and feedback on this software platform as users engage with it. One of the challenges with reviewing this manuscript is that, while I spent a bit of time playing with the software, it is challenging to provide specific feedback on its strengths or deficiencies without actually using it in practice for a specific disease and programmatic analysis. As such, I think ongoing public feedback on the software from actual users is more critical than peer review of this manuscript. We thank the reviewer for this excellent suggestion. We have added a blog to our website (where we can also post information on updates to the tool). Users can provide feedback via the comments section.

Care cascades for different diseases deal with transitions differently. For example, most HIV care cascades look at transitions backwards as well as forwards across stages (or "compartments"). In contrast, in most care cascades for active TB, patients can only move forward across care cascade stages, and they can have multiple types of poor outcomes in each "gap" (i.e., difference between steps / stages / compartments). For example, for patients who start treatment but do not complete TB treatment, they could have one of 3 poor outcomes: (a) death, (b) treatment failure, and (c) loss to follow-up. The assumption is that "loss to follow-up" patients do not move "backwards" in the care cascade but fall out completely (and would have to restart from the beginning). Two questions related to this: (a) can this software modeling approach manage care cascades that only have transitions in the forward direction (I am assuming yes from Fig 3, but would be helpful to clarify); and (b) can this software modeling approach capture and estimate different types of poor outcomes as described above? Clarifying both of these questions in the text would be helpful for readers coming from different disease backgrounds and envisioning the approach differently. Yes, both types of cascade can be modelled with the tool. We have added text on this to the methods section.

A key point in the manuscript is this statement: "In many real-world situations, the impact of changing intervention coverage and the way interventions should be prioritized is not clear from the analysis of intervention properties alone." This is an important point that may not be evident to readers who don't frequently look at modeling data that look at broader implications and impacts of interventions. When I read this, I had a few thoughts regarding how the authors could expand on this point:

It would be helpful for the authors to add a few sentences explaining this point further. If we already have data on a particular intervention and its impact on reducing a given gap in care, what are the additional benefits of the type of modeling proposed by the authors?

One practical problem that users of this software will face may be the lack of available data on the effect sizes and costing of different interventions to reduce gaps in care. It would be helpful for the authors to specify what types of data / findings users of the software should have available to use this tool. Do they need effect sizes of an intervention to reduce a gap in the care cascade (i.e., estimated % reduction in a poor outcome at a particular step from an intervention)? Do they need confidence intervals for this effect estimate? Do they need these effect size estimates for an intervention for multiple care cascade steps (if an intervention improves outcomes at multiple steps)? What kind of costing data do they need to use this tool?

Finally, it would be helpful for the authors to provide some real world examples of the types of studies that are available from which users of the software can provide these estimates. Even providing citations, example effect sizes or costing data from the existing literature for studies from HIV (for example, since they are most broadly available here) would help readers to think about the types of data they can seek out for their own diseases to populate these models.

We have:

Moved this text to a more prominent position in the article, and emphasized it more clearly by repeating it in the discussion section as well.

“One practical problem that users of this software will face may be the lack of available data on the effect sizes and costing of different interventions to reduce gaps in care.” -- we added a section noting the issues related to data availability in the methods.

“It would be helpful for the authors to specify what types of data / findings users of the software should have available to use this tool.” - we added a section on minimum data requirements to the data entry section of the methods

“Do they need effect sizes of an intervention to reduce a gap in the care cascade (i.e., estimated % reduction in a poor outcome at a particular step from an intervention)” -- yes, this is needed, and we’ve added text clarifying this.

“Do they need confidence intervals for this effect estimate?” -- this is not required.

“Do they need these effect size estimates for an intervention for multiple care cascade steps (if an intervention improves outcomes at multiple steps)? What kind of costing data do they need to use this tool?” - we have specified this in the data entry section.

We have added a paragraph on typical data sources.

Authors might consider including a citation for the Lancet Global Health Commission on High-Quality Health Systems, as that major report has argued for care cascade analyses as being a central component of health quality dashboards for understanding quality of care. This strengthens the argument for a user friendly tool such as the one created by these authors. Thank you, we have added this.

In paragraph 2 of the paper, the authors should also note that the phrase "continuum of care" has also been used for these types of analyses. This is now emerging as the predominant language for these analyses in HIV, with the assumption that patients can move backwards as well as forwards along this continuum of care. Thank you, we have added this.

Paragraph 3 of the Introduction: The authors can correct the way they have described the TB care cascade analyses. The India and South Africa care cascades that have been cited for TB look at active TB disease, while the latent TB care cascade cited looks at latent TB disease. As such, these are two different frameworks for different types of TB--i.e., it is not that the framework in citation 10 guides the framework in citations 11 and 12--they are different frameworks for different forms of TB. A more detailed methods framework for active TB disease is available in the manuscript: Subbaraman R, Nathavitharana RR, Mayer KH, Satyanarayana S, Chadha VK, Arinaminpathy N, et al. (2019) Constructing care cascades for active tuberculosis: A strategy for program monitoring and identifying gaps in quality of care1. Such methodological manuscripts could inform development of models using a tool such as the one the authors have created. Thank you, we have fixed this and added the suggested citation.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 13 Jan 2020

Robyn Stuart, Department of Mathematical Sciences, University of Copenhagen, Universitetsparken 5, Copenhagen, 2100, Denmark

13 Jan 2020

Author Response
- Ideally, there would be some platform for public comment, critique, and feedback on this software platform as users engage with it. One of the challenges with reviewing this
... Continue reading
Ideally, there would be some platform for public comment, critique, and feedback on this software platform as users engage with it. One of the challenges with reviewing this manuscript is that, while I spent a bit of time playing with the software, it is challenging to provide specific feedback on its strengths or deficiencies without actually using it in practice for a specific disease and programmatic analysis. As such, I think ongoing public feedback on the software from actual users is more critical than peer review of this manuscript. We thank the reviewer for this excellent suggestion. We have added a blog to our website (where we can also post information on updates to the tool). Users can provide feedback via the comments section.

Care cascades for different diseases deal with transitions differently. For example, most HIV care cascades look at transitions backwards as well as forwards across stages (or "compartments"). In contrast, in most care cascades for active TB, patients can only move forward across care cascade stages, and they can have multiple types of poor outcomes in each "gap" (i.e., difference between steps / stages / compartments). For example, for patients who start treatment but do not complete TB treatment, they could have one of 3 poor outcomes: (a) death, (b) treatment failure, and (c) loss to follow-up. The assumption is that "loss to follow-up" patients do not move "backwards" in the care cascade but fall out completely (and would have to restart from the beginning). Two questions related to this: (a) can this software modeling approach manage care cascades that only have transitions in the forward direction (I am assuming yes from Fig 3, but would be helpful to clarify); and (b) can this software modeling approach capture and estimate different types of poor outcomes as described above? Clarifying both of these questions in the text would be helpful for readers coming from different disease backgrounds and envisioning the approach differently. Yes, both types of cascade can be modelled with the tool. We have added text on this to the methods section.

A key point in the manuscript is this statement: "In many real-world situations, the impact of changing intervention coverage and the way interventions should be prioritized is not clear from the analysis of intervention properties alone." This is an important point that may not be evident to readers who don't frequently look at modeling data that look at broader implications and impacts of interventions. When I read this, I had a few thoughts regarding how the authors could expand on this point:

It would be helpful for the authors to add a few sentences explaining this point further. If we already have data on a particular intervention and its impact on reducing a given gap in care, what are the additional benefits of the type of modeling proposed by the authors?

One practical problem that users of this software will face may be the lack of available data on the effect sizes and costing of different interventions to reduce gaps in care. It would be helpful for the authors to specify what types of data / findings users of the software should have available to use this tool. Do they need effect sizes of an intervention to reduce a gap in the care cascade (i.e., estimated % reduction in a poor outcome at a particular step from an intervention)? Do they need confidence intervals for this effect estimate? Do they need these effect size estimates for an intervention for multiple care cascade steps (if an intervention improves outcomes at multiple steps)? What kind of costing data do they need to use this tool?

Finally, it would be helpful for the authors to provide some real world examples of the types of studies that are available from which users of the software can provide these estimates. Even providing citations, example effect sizes or costing data from the existing literature for studies from HIV (for example, since they are most broadly available here) would help readers to think about the types of data they can seek out for their own diseases to populate these models.

We have:

Moved this text to a more prominent position in the article, and emphasized it more clearly by repeating it in the discussion section as well.

“One practical problem that users of this software will face may be the lack of available data on the effect sizes and costing of different interventions to reduce gaps in care.” -- we added a section noting the issues related to data availability in the methods.

“It would be helpful for the authors to specify what types of data / findings users of the software should have available to use this tool.” - we added a section on minimum data requirements to the data entry section of the methods

“Do they need effect sizes of an intervention to reduce a gap in the care cascade (i.e., estimated % reduction in a poor outcome at a particular step from an intervention)” -- yes, this is needed, and we’ve added text clarifying this.

“Do they need confidence intervals for this effect estimate?” -- this is not required.

“Do they need these effect size estimates for an intervention for multiple care cascade steps (if an intervention improves outcomes at multiple steps)? What kind of costing data do they need to use this tool?” - we have specified this in the data entry section.

We have added a paragraph on typical data sources.

Authors might consider including a citation for the Lancet Global Health Commission on High-Quality Health Systems, as that major report has argued for care cascade analyses as being a central component of health quality dashboards for understanding quality of care. This strengthens the argument for a user friendly tool such as the one created by these authors. Thank you, we have added this.

In paragraph 2 of the paper, the authors should also note that the phrase "continuum of care" has also been used for these types of analyses. This is now emerging as the predominant language for these analyses in HIV, with the assumption that patients can move backwards as well as forwards along this continuum of care. Thank you, we have added this.

Paragraph 3 of the Introduction: The authors can correct the way they have described the TB care cascade analyses. The India and South Africa care cascades that have been cited for TB look at active TB disease, while the latent TB care cascade cited looks at latent TB disease. As such, these are two different frameworks for different types of TB--i.e., it is not that the framework in citation 10 guides the framework in citations 11 and 12--they are different frameworks for different forms of TB. A more detailed methods framework for active TB disease is available in the manuscript: Subbaraman R, Nathavitharana RR, Mayer KH, Satyanarayana S, Chadha VK, Arinaminpathy N, et al. (2019) Constructing care cascades for active tuberculosis: A strategy for program monitoring and identifying gaps in quality of care1. Such methodological manuscripts could inform development of models using a tool such as the one the authors have created. Thank you, we have fixed this and added the suggested citation.
Ideally, there would be some platform for public comment, critique, and feedback on this software platform as users engage with it. One of the challenges with reviewing this manuscript is that, while I spent a bit of time playing with the software, it is challenging to provide specific feedback on its strengths or deficiencies without actually using it in practice for a specific disease and programmatic analysis. As such, I think ongoing public feedback on the software from actual users is more critical than peer review of this manuscript. We thank the reviewer for this excellent suggestion. We have added a blog to our website (where we can also post information on updates to the tool). Users can provide feedback via the comments section.

Care cascades for different diseases deal with transitions differently. For example, most HIV care cascades look at transitions backwards as well as forwards across stages (or "compartments"). In contrast, in most care cascades for active TB, patients can only move forward across care cascade stages, and they can have multiple types of poor outcomes in each "gap" (i.e., difference between steps / stages / compartments). For example, for patients who start treatment but do not complete TB treatment, they could have one of 3 poor outcomes: (a) death, (b) treatment failure, and (c) loss to follow-up. The assumption is that "loss to follow-up" patients do not move "backwards" in the care cascade but fall out completely (and would have to restart from the beginning). Two questions related to this: (a) can this software modeling approach manage care cascades that only have transitions in the forward direction (I am assuming yes from Fig 3, but would be helpful to clarify); and (b) can this software modeling approach capture and estimate different types of poor outcomes as described above? Clarifying both of these questions in the text would be helpful for readers coming from different disease backgrounds and envisioning the approach differently. Yes, both types of cascade can be modelled with the tool. We have added text on this to the methods section.

A key point in the manuscript is this statement: "In many real-world situations, the impact of changing intervention coverage and the way interventions should be prioritized is not clear from the analysis of intervention properties alone." This is an important point that may not be evident to readers who don't frequently look at modeling data that look at broader implications and impacts of interventions. When I read this, I had a few thoughts regarding how the authors could expand on this point:

It would be helpful for the authors to add a few sentences explaining this point further. If we already have data on a particular intervention and its impact on reducing a given gap in care, what are the additional benefits of the type of modeling proposed by the authors?

One practical problem that users of this software will face may be the lack of available data on the effect sizes and costing of different interventions to reduce gaps in care. It would be helpful for the authors to specify what types of data / findings users of the software should have available to use this tool. Do they need effect sizes of an intervention to reduce a gap in the care cascade (i.e., estimated % reduction in a poor outcome at a particular step from an intervention)? Do they need confidence intervals for this effect estimate? Do they need these effect size estimates for an intervention for multiple care cascade steps (if an intervention improves outcomes at multiple steps)? What kind of costing data do they need to use this tool?

Finally, it would be helpful for the authors to provide some real world examples of the types of studies that are available from which users of the software can provide these estimates. Even providing citations, example effect sizes or costing data from the existing literature for studies from HIV (for example, since they are most broadly available here) would help readers to think about the types of data they can seek out for their own diseases to populate these models.

We have:

Moved this text to a more prominent position in the article, and emphasized it more clearly by repeating it in the discussion section as well.

“One practical problem that users of this software will face may be the lack of available data on the effect sizes and costing of different interventions to reduce gaps in care.” -- we added a section noting the issues related to data availability in the methods.

“It would be helpful for the authors to specify what types of data / findings users of the software should have available to use this tool.” - we added a section on minimum data requirements to the data entry section of the methods

“Do they need effect sizes of an intervention to reduce a gap in the care cascade (i.e., estimated % reduction in a poor outcome at a particular step from an intervention)” -- yes, this is needed, and we’ve added text clarifying this.

“Do they need confidence intervals for this effect estimate?” -- this is not required.

“Do they need these effect size estimates for an intervention for multiple care cascade steps (if an intervention improves outcomes at multiple steps)? What kind of costing data do they need to use this tool?” - we have specified this in the data entry section.

We have added a paragraph on typical data sources.

Authors might consider including a citation for the Lancet Global Health Commission on High-Quality Health Systems, as that major report has argued for care cascade analyses as being a central component of health quality dashboards for understanding quality of care. This strengthens the argument for a user friendly tool such as the one created by these authors. Thank you, we have added this.

In paragraph 2 of the paper, the authors should also note that the phrase "continuum of care" has also been used for these types of analyses. This is now emerging as the predominant language for these analyses in HIV, with the assumption that patients can move backwards as well as forwards along this continuum of care. Thank you, we have added this.

Paragraph 3 of the Introduction: The authors can correct the way they have described the TB care cascade analyses. The India and South Africa care cascades that have been cited for TB look at active TB disease, while the latent TB care cascade cited looks at latent TB disease. As such, these are two different frameworks for different types of TB--i.e., it is not that the framework in citation 10 guides the framework in citations 11 and 12--they are different frameworks for different forms of TB. A more detailed methods framework for active TB disease is available in the manuscript: Subbaraman R, Nathavitharana RR, Mayer KH, Satyanarayana S, Chadha VK, Arinaminpathy N, et al. (2019) Constructing care cascades for active tuberculosis: A strategy for program monitoring and identifying gaps in quality of care1. Such methodological manuscripts could inform development of models using a tool such as the one the authors have created. Thank you, we have fixed this and added the suggested citation.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Views

Reviewer Report 25 Jun 2019

Noah Haber, Carolina Population Center, University of North Carolina at Chapel Hill, Chapel Hill, NC, USA; Meta-Research Innovation Center, Stanford University, Stanford, CA, USA

Approved with Reservations

https://doi.org/10.21956/gatesopenres.14141.r27336

General comments
I believe that this software appears to be a strong and useful effort toward making useful decisions based on cascades, under a generalized framework. The authors have identified an important problem, and have made substantial progress towards providing a useful solution. As a preliminary and experimental release, I believe this to be a successful effort. However, some caveats should be considered with regard to the software and its accompanying paper as they currently stand.

A general concern is that software is requires a high degree of sophistication and understanding of data and modelling to work as intended. The effort and sophistication required is highlighted in the example, where the assumptions required are often very serious, and highly consequential.

In addition, the report as it stands could be more clearly organized and give additional technical detail in the methods section.

As the authors note, it shows promise and potential. Getting it from a proof of concept that solves very interesting problems to being useful/usable to relatively novice users is long process. I really hope that this effort continues to develop into maturity.

Methods
General comments: I would suggest a fairly substantial re-organization for this section. Quite a bit of time is spent on introducing people to the concept of a cascade (which is not the innovative part of this paper), at the expense of what is useful, interesting, and innovative about this tool.

The section reads like a manual for designing a cascade analysis with the tool, rather than an explanation of what the software actually does and the methods and math underlying it. Quite a few sections are not the software methods at all, and should be moved to the introduction or removed. I am not sure I would be able to recreate a near equivalent of this tool without much more detail on the underlying model itself.

I found that I did not understand how the model actually functioned, beyond that it was a compartmental model. Showing some of the math a bit more (even as an example, or just citations) would go a long way toward helping understand what's going on.

Designing the cascade
I think the language used for this framework could use a major revisit. It took me quite a bit of time and going backward to figure out what the authors were referring to throughout, which was distracting for the later sections.

In the context of the user-oriented manual view, referring to the stages as "compartments" seems out of place and unnecessary, when "stage" or "state" seems more appropriate and more general for users. If this is an explanation of the methods of the model, then saying it is based on a compartmental model (and specifying exactly how said model is parameterized) is useful.

"Parameter" has a much broader meaning, and forcing "parameter" to mean this very specific thing, is confusing. I would suggest referring to this as "transition properties" or "transition parameters" and collapse this paragraph with the previous. Also, what, specifically are the required parameters, and in what units? At minimum, transition rates need to be entered, correct?

The same applies to the word "characteristics". Why not just use "stage groups" or similar?

Collecting data
Again, a bit strange here. Data entry and data collection are two different things. Which are the authors trying to describe, and do they belong in the methods or in the use example? As an aside, I find the Excel interface bit difficult to use, and unintuitive why I would have to exit the site to enter data. It would be far more straightforward to have a browser-based UI for this, with optional support for Excel-based data entry.

Analysis of policy questions
I believe that this belongs in the intro.

Cascade optimization
This is where the good stuff is! Lead with this, shorten/consolidate/remove the rest. I found this section to be relatively clear and well-written, but unfortunately buried underneath everything else.

Example cascade
One thing this section really highlights is the incredible amount of sophisticated work users need to do to make all this work together. Possibly to the point that a user who is able to adequately generate these numbers could very nearly model this all themselves. This is a first major effort, so that is to be expected, but it should be considered strongly.

It would be helpful if this was more obviously linked to the compartments. Example: We estimated the transition rate from stage X to stage Y by ____.

"We further assume that the hypertension cascade is in a steady state such that the relative proportions of people in each cascade stage are constant over time, which implies that the number of people in each cascade stage will increase by 4.4% each year."

This is a suspect and (as far as I can tell) unnecessary assumption. If this were true, there would be no change in the proportions between years (which there are, as shown in Figure 4). Why not use between-year flow rates (noting a few minor assumptions)? I might suggest that adding a mini model to solve for those flow rates would be an extremely useful feature, as forcing users to do this on their own will be error-prone. While is just an example, but it's a potentially distracting error.

Discussion
I would suggest that the discussion section have a much more comprehensive treatment of limitations of the tool. What kinds of things can it not model? Am I able to create a fully fledged SIR model, for example? That might be implied by the use of compartment modelling, it isn't clear to me whether or not this is possible.

One clear limitation of this model is that it has a bit of a strange relationship with time. A slightly pedantic issue is that the authors appear to be using rates and probabilities interchangeably. More importantly, enormous assumptions must be made in order to turn the cross-sectional data sources into what appears to be models over time. Issues in these assumptions and pre-model modelling can lead to severe misallocation of resources.

I believe this to be a useful tool, albeit one that would benefit greatly from real-world testing, and I hope that the authors are able to continue developing it.

Is the rationale for developing the new software tool clearly explained?

Yes
Is the description of the software tool technically sound?

Yes
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Partly
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Yes
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Partly

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: HIV, cascades, global health

CITE

Report a concern

Author Response 13 Jan 2020

Robyn Stuart, Department of Mathematical Sciences, University of Copenhagen, Universitetsparken 5, Copenhagen, 2100, Denmark

13 Jan 2020

Author Response
- I believe that this software appears to be a strong and useful effort toward making useful decisions based on cascades, under a generalized framework. The authors have identified
... Continue reading
I believe that this software appears to be a strong and useful effort toward making useful decisions based on cascades, under a generalized framework. The authors have identified an important problem, and have made substantial progress towards providing a useful solution. As a preliminary and experimental release, I believe this to be a successful effort. However, some caveats should be considered with regard to the software and its accompanying paper as they currently stand. We thank the reviewer for the summary.

A general concern is that software requires a high degree of sophistication and understanding of data and modelling to work as intended. The effort and sophistication required is highlighted in the example, where the assumptions required are often very serious, and highly consequential. This is well noted, and in response to this comment we have (a) revised the manuscript so it caters to a less technically knowledgeable audience, and (b) added text summarizing these concerns raised by the reviewer to the limitations paragraph of the discussion section.

In addition, the report as it stands could be more clearly organized and give additional technical detail in the methods section. We have attempted to streamline and clarify the methods section (also in response to comments from the other reviewers).

As the authors note, it shows promise and potential. Getting it from a proof of concept that solves very interesting problems to being useful/usable to relatively novice users is a long process. I really hope that this effort continues to develop into maturity. We thank the reviewer for the kind words and well wishes. As per a comment from the second reviewer, we have established a mechanism for gathering user feedback. We are looking forward to further improving our software in response to user comments.

Methods General comments: I would suggest a fairly substantial re-organization for this section. Quite a bit of time is spent on introducing people to the concept of a cascade (which is not the innovative part of this paper), at the expense of what is useful, interesting, and innovative about this tool. The section reads like a manual for designing a cascade analysis with the tool, rather than an explanation of what the software actually does and the methods and math underlying it. Quite a few sections are not the software methods at all, and should be moved to the introduction or removed. I am not sure I would be able to recreate a near equivalent of this tool without much more detail on the underlying model itself. I found that I did not understand how the model actually functioned, beyond that it was a compartmental model. Showing some of the math a bit more (even as an example, or just citations) would go a long way toward helping understand what's going on.We have rearranged this section significantly. Firstly, we have expanded the section on implementation (NB - the section headings are taken from the article guidelines on how software tool articles should be structured). The reviewer makes a good point that we were previously lacking detail on how the software is actually structured, so we have added this to the implementation section. Creating a similar tool would be possible by following the architecture in Figure 3. Much of the math behind the model is actually handled by the Atomica package, and we don’t go into detail about it here. However, we’ve added more detail in the example.

Designing the cascade: I think the language used for this framework could use a major revisit. It took me quite a bit of time and going backward to figure out what the authors were referring to throughout, which was distracting for the later sections. In the context of the user-oriented manual view, referring to the stages as "compartments" seems out of place and unnecessary, when "stage" or "state" seems more appropriate and more general for users. If this is an explanation of the methods of the model, then saying it is based on a compartmental model (and specifying exactly how said model is parameterized) is useful. "Parameter" has a much broader meaning, and forcing "parameter" to mean this very specific thing, is confusing. I would suggest referring to this as "transition properties" or "transition parameters" and collapse this paragraph with the previous. Also, what, specifically are the required parameters, and in what units? At minimum, transition rates need to be entered, correct? The same applies to the word "characteristics". Why not just use "stage groups" or similar? We have reworded this section (also noted in the comments from the two other reviewers). We wish to emphasize the connection between the cascade modelling methodology and compartmental models, so we have retained “compartment” and “transition”. We have also retained “parameter”, even though we agree it has a very broad meaning, because it is heavily entwined in the software itself and is used with internal consistency in this article. However, we have removed “characteristics” (also noted by another reviewer), and we have written a paragraph on the minimal data requirements. We intend for this section to help readers understand the relationship between a compartmental model and a cascade representation.

Collecting data: Again, a bit strange here. Data entry and data collection are two different things. Which are the authors trying to describe, and do they belong in the methods or in the use example? As an aside, I find the Excel interface bit difficult to use, and unintuitive why I would have to exit the site to enter data. It would be far more straightforward to have a browser-based UI for this, with optional support for Excel-based data entry. We renamed this section “Data entry”. We experimented with the idea of having users enter data via the web application itself, but experience with users led us to understand that people are very accustomed to entering data via Excel, and that doing so allows them to more easily share files with colleagues and collaborate effectively. In the end, we decided to offer Excel support since that’s what most users seemed to want.

Analysis of policy questions: I believe that this belongs in the intro. We have shifted this to the intro.

Cascade optimization: This is where the good stuff is! Lead with this, shorten/consolidate/remove the rest. I found this section to be relatively clear and well-written, but unfortunately buried underneath everything else. We have shortened the rest of the “Operation” section of the methods (again, this is a required section heading for this article type), so that this is placed more prominently in the methods.

Example cascade: One thing this section really highlights is the incredible amount of sophisticated work users need to do to make all this work together. Possibly to the point that a user who is able to adequately generate these numbers could very nearly model this all themselves. This is a first major effort, so that is to be expected, but it should be considered strongly. It would be helpful if this was more obviously linked to the compartments. Example: We estimated the transition rate from stage X to stage Y by ____. In our experience, it is not uncommon for people to have access to all the data summarized in this example section, but not to know how to combine it and analyze it to get policy recommendations.

"We further assume that the hypertension cascade is in a steady state such that the relative proportions of people in each cascade stage are constant over time, which implies that the number of people in each cascade stage will increase by 4.4% each year." This is a suspect and (as far as I can tell) unnecessary assumption. If this were true, there would be no change in the proportions between years (which there are, as shown in Figure 4). Why not use between-year flow rates (noting a few minor assumptions)? I might suggest that adding a mini model to solve for those flow rates would be an extremely useful feature, as forcing users to do this on their own will be error-prone. While is just an example, but it's a potentially distracting error. We have removed this.

Discussion: I would suggest that the discussion section have a much more comprehensive treatment of limitations of the tool. What kinds of things can it not model? Am I able to create a fully fledged SIR model, for example? That might be implied by the use of compartment modelling, it isn't clear to me whether or not this is possible. We have added a paragraph on limitations.

One clear limitation of this model is that it has a bit of a strange relationship with time. A slightly pedantic issue is that the authors appear to be using rates and probabilities interchangeably. More importantly, enormous assumptions must be made in order to turn the cross-sectional data sources into what appears to be models over time. Issues in these assumptions and pre-model modelling can lead to severe misallocation of resources. It’s a very good point (not pedantic!) about rates vs probabilities - we have clarified this throughout. We have also added text in the limitations paragraph of the discussion section on the potential issues related to using single time-points as data sources for inform time-dependent estimates.

I believe this to be a useful tool, albeit one that would benefit greatly from real-world testing, and I hope that the authors are able to continue developing it. Thank you for taking the time to review!
I believe that this software appears to be a strong and useful effort toward making useful decisions based on cascades, under a generalized framework. The authors have identified an important problem, and have made substantial progress towards providing a useful solution. As a preliminary and experimental release, I believe this to be a successful effort. However, some caveats should be considered with regard to the software and its accompanying paper as they currently stand. We thank the reviewer for the summary.

A general concern is that software requires a high degree of sophistication and understanding of data and modelling to work as intended. The effort and sophistication required is highlighted in the example, where the assumptions required are often very serious, and highly consequential. This is well noted, and in response to this comment we have (a) revised the manuscript so it caters to a less technically knowledgeable audience, and (b) added text summarizing these concerns raised by the reviewer to the limitations paragraph of the discussion section.

In addition, the report as it stands could be more clearly organized and give additional technical detail in the methods section. We have attempted to streamline and clarify the methods section (also in response to comments from the other reviewers).

As the authors note, it shows promise and potential. Getting it from a proof of concept that solves very interesting problems to being useful/usable to relatively novice users is a long process. I really hope that this effort continues to develop into maturity. We thank the reviewer for the kind words and well wishes. As per a comment from the second reviewer, we have established a mechanism for gathering user feedback. We are looking forward to further improving our software in response to user comments.

Methods General comments: I would suggest a fairly substantial re-organization for this section. Quite a bit of time is spent on introducing people to the concept of a cascade (which is not the innovative part of this paper), at the expense of what is useful, interesting, and innovative about this tool. The section reads like a manual for designing a cascade analysis with the tool, rather than an explanation of what the software actually does and the methods and math underlying it. Quite a few sections are not the software methods at all, and should be moved to the introduction or removed. I am not sure I would be able to recreate a near equivalent of this tool without much more detail on the underlying model itself. I found that I did not understand how the model actually functioned, beyond that it was a compartmental model. Showing some of the math a bit more (even as an example, or just citations) would go a long way toward helping understand what's going on.We have rearranged this section significantly. Firstly, we have expanded the section on implementation (NB - the section headings are taken from the article guidelines on how software tool articles should be structured). The reviewer makes a good point that we were previously lacking detail on how the software is actually structured, so we have added this to the implementation section. Creating a similar tool would be possible by following the architecture in Figure 3. Much of the math behind the model is actually handled by the Atomica package, and we don’t go into detail about it here. However, we’ve added more detail in the example.

Designing the cascade: I think the language used for this framework could use a major revisit. It took me quite a bit of time and going backward to figure out what the authors were referring to throughout, which was distracting for the later sections. In the context of the user-oriented manual view, referring to the stages as "compartments" seems out of place and unnecessary, when "stage" or "state" seems more appropriate and more general for users. If this is an explanation of the methods of the model, then saying it is based on a compartmental model (and specifying exactly how said model is parameterized) is useful. "Parameter" has a much broader meaning, and forcing "parameter" to mean this very specific thing, is confusing. I would suggest referring to this as "transition properties" or "transition parameters" and collapse this paragraph with the previous. Also, what, specifically are the required parameters, and in what units? At minimum, transition rates need to be entered, correct? The same applies to the word "characteristics". Why not just use "stage groups" or similar? We have reworded this section (also noted in the comments from the two other reviewers). We wish to emphasize the connection between the cascade modelling methodology and compartmental models, so we have retained “compartment” and “transition”. We have also retained “parameter”, even though we agree it has a very broad meaning, because it is heavily entwined in the software itself and is used with internal consistency in this article. However, we have removed “characteristics” (also noted by another reviewer), and we have written a paragraph on the minimal data requirements. We intend for this section to help readers understand the relationship between a compartmental model and a cascade representation.

Collecting data: Again, a bit strange here. Data entry and data collection are two different things. Which are the authors trying to describe, and do they belong in the methods or in the use example? As an aside, I find the Excel interface bit difficult to use, and unintuitive why I would have to exit the site to enter data. It would be far more straightforward to have a browser-based UI for this, with optional support for Excel-based data entry. We renamed this section “Data entry”. We experimented with the idea of having users enter data via the web application itself, but experience with users led us to understand that people are very accustomed to entering data via Excel, and that doing so allows them to more easily share files with colleagues and collaborate effectively. In the end, we decided to offer Excel support since that’s what most users seemed to want.

Analysis of policy questions: I believe that this belongs in the intro. We have shifted this to the intro.

Cascade optimization: This is where the good stuff is! Lead with this, shorten/consolidate/remove the rest. I found this section to be relatively clear and well-written, but unfortunately buried underneath everything else. We have shortened the rest of the “Operation” section of the methods (again, this is a required section heading for this article type), so that this is placed more prominently in the methods.

Example cascade: One thing this section really highlights is the incredible amount of sophisticated work users need to do to make all this work together. Possibly to the point that a user who is able to adequately generate these numbers could very nearly model this all themselves. This is a first major effort, so that is to be expected, but it should be considered strongly. It would be helpful if this was more obviously linked to the compartments. Example: We estimated the transition rate from stage X to stage Y by ____. In our experience, it is not uncommon for people to have access to all the data summarized in this example section, but not to know how to combine it and analyze it to get policy recommendations.

"We further assume that the hypertension cascade is in a steady state such that the relative proportions of people in each cascade stage are constant over time, which implies that the number of people in each cascade stage will increase by 4.4% each year." This is a suspect and (as far as I can tell) unnecessary assumption. If this were true, there would be no change in the proportions between years (which there are, as shown in Figure 4). Why not use between-year flow rates (noting a few minor assumptions)? I might suggest that adding a mini model to solve for those flow rates would be an extremely useful feature, as forcing users to do this on their own will be error-prone. While is just an example, but it's a potentially distracting error. We have removed this.

Discussion: I would suggest that the discussion section have a much more comprehensive treatment of limitations of the tool. What kinds of things can it not model? Am I able to create a fully fledged SIR model, for example? That might be implied by the use of compartment modelling, it isn't clear to me whether or not this is possible. We have added a paragraph on limitations.

One clear limitation of this model is that it has a bit of a strange relationship with time. A slightly pedantic issue is that the authors appear to be using rates and probabilities interchangeably. More importantly, enormous assumptions must be made in order to turn the cross-sectional data sources into what appears to be models over time. Issues in these assumptions and pre-model modelling can lead to severe misallocation of resources. It’s a very good point (not pedantic!) about rates vs probabilities - we have clarified this throughout. We have also added text in the limitations paragraph of the discussion section on the potential issues related to using single time-points as data sources for inform time-dependent estimates.

I believe this to be a useful tool, albeit one that would benefit greatly from real-world testing, and I hope that the authors are able to continue developing it. Thank you for taking the time to review!
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 13 Jan 2020

Robyn Stuart, Department of Mathematical Sciences, University of Copenhagen, Universitetsparken 5, Copenhagen, 2100, Denmark

13 Jan 2020

Author Response
- I believe that this software appears to be a strong and useful effort toward making useful decisions based on cascades, under a generalized framework. The authors have identified
... Continue reading
I believe that this software appears to be a strong and useful effort toward making useful decisions based on cascades, under a generalized framework. The authors have identified an important problem, and have made substantial progress towards providing a useful solution. As a preliminary and experimental release, I believe this to be a successful effort. However, some caveats should be considered with regard to the software and its accompanying paper as they currently stand. We thank the reviewer for the summary.

A general concern is that software requires a high degree of sophistication and understanding of data and modelling to work as intended. The effort and sophistication required is highlighted in the example, where the assumptions required are often very serious, and highly consequential. This is well noted, and in response to this comment we have (a) revised the manuscript so it caters to a less technically knowledgeable audience, and (b) added text summarizing these concerns raised by the reviewer to the limitations paragraph of the discussion section.

In addition, the report as it stands could be more clearly organized and give additional technical detail in the methods section. We have attempted to streamline and clarify the methods section (also in response to comments from the other reviewers).

As the authors note, it shows promise and potential. Getting it from a proof of concept that solves very interesting problems to being useful/usable to relatively novice users is a long process. I really hope that this effort continues to develop into maturity. We thank the reviewer for the kind words and well wishes. As per a comment from the second reviewer, we have established a mechanism for gathering user feedback. We are looking forward to further improving our software in response to user comments.

Methods General comments: I would suggest a fairly substantial re-organization for this section. Quite a bit of time is spent on introducing people to the concept of a cascade (which is not the innovative part of this paper), at the expense of what is useful, interesting, and innovative about this tool. The section reads like a manual for designing a cascade analysis with the tool, rather than an explanation of what the software actually does and the methods and math underlying it. Quite a few sections are not the software methods at all, and should be moved to the introduction or removed. I am not sure I would be able to recreate a near equivalent of this tool without much more detail on the underlying model itself. I found that I did not understand how the model actually functioned, beyond that it was a compartmental model. Showing some of the math a bit more (even as an example, or just citations) would go a long way toward helping understand what's going on.We have rearranged this section significantly. Firstly, we have expanded the section on implementation (NB - the section headings are taken from the article guidelines on how software tool articles should be structured). The reviewer makes a good point that we were previously lacking detail on how the software is actually structured, so we have added this to the implementation section. Creating a similar tool would be possible by following the architecture in Figure 3. Much of the math behind the model is actually handled by the Atomica package, and we don’t go into detail about it here. However, we’ve added more detail in the example.

Designing the cascade: I think the language used for this framework could use a major revisit. It took me quite a bit of time and going backward to figure out what the authors were referring to throughout, which was distracting for the later sections. In the context of the user-oriented manual view, referring to the stages as "compartments" seems out of place and unnecessary, when "stage" or "state" seems more appropriate and more general for users. If this is an explanation of the methods of the model, then saying it is based on a compartmental model (and specifying exactly how said model is parameterized) is useful. "Parameter" has a much broader meaning, and forcing "parameter" to mean this very specific thing, is confusing. I would suggest referring to this as "transition properties" or "transition parameters" and collapse this paragraph with the previous. Also, what, specifically are the required parameters, and in what units? At minimum, transition rates need to be entered, correct? The same applies to the word "characteristics". Why not just use "stage groups" or similar? We have reworded this section (also noted in the comments from the two other reviewers). We wish to emphasize the connection between the cascade modelling methodology and compartmental models, so we have retained “compartment” and “transition”. We have also retained “parameter”, even though we agree it has a very broad meaning, because it is heavily entwined in the software itself and is used with internal consistency in this article. However, we have removed “characteristics” (also noted by another reviewer), and we have written a paragraph on the minimal data requirements. We intend for this section to help readers understand the relationship between a compartmental model and a cascade representation.

Collecting data: Again, a bit strange here. Data entry and data collection are two different things. Which are the authors trying to describe, and do they belong in the methods or in the use example? As an aside, I find the Excel interface bit difficult to use, and unintuitive why I would have to exit the site to enter data. It would be far more straightforward to have a browser-based UI for this, with optional support for Excel-based data entry. We renamed this section “Data entry”. We experimented with the idea of having users enter data via the web application itself, but experience with users led us to understand that people are very accustomed to entering data via Excel, and that doing so allows them to more easily share files with colleagues and collaborate effectively. In the end, we decided to offer Excel support since that’s what most users seemed to want.

Analysis of policy questions: I believe that this belongs in the intro. We have shifted this to the intro.

Cascade optimization: This is where the good stuff is! Lead with this, shorten/consolidate/remove the rest. I found this section to be relatively clear and well-written, but unfortunately buried underneath everything else. We have shortened the rest of the “Operation” section of the methods (again, this is a required section heading for this article type), so that this is placed more prominently in the methods.

Example cascade: One thing this section really highlights is the incredible amount of sophisticated work users need to do to make all this work together. Possibly to the point that a user who is able to adequately generate these numbers could very nearly model this all themselves. This is a first major effort, so that is to be expected, but it should be considered strongly. It would be helpful if this was more obviously linked to the compartments. Example: We estimated the transition rate from stage X to stage Y by ____. In our experience, it is not uncommon for people to have access to all the data summarized in this example section, but not to know how to combine it and analyze it to get policy recommendations.

"We further assume that the hypertension cascade is in a steady state such that the relative proportions of people in each cascade stage are constant over time, which implies that the number of people in each cascade stage will increase by 4.4% each year." This is a suspect and (as far as I can tell) unnecessary assumption. If this were true, there would be no change in the proportions between years (which there are, as shown in Figure 4). Why not use between-year flow rates (noting a few minor assumptions)? I might suggest that adding a mini model to solve for those flow rates would be an extremely useful feature, as forcing users to do this on their own will be error-prone. While is just an example, but it's a potentially distracting error. We have removed this.

Discussion: I would suggest that the discussion section have a much more comprehensive treatment of limitations of the tool. What kinds of things can it not model? Am I able to create a fully fledged SIR model, for example? That might be implied by the use of compartment modelling, it isn't clear to me whether or not this is possible. We have added a paragraph on limitations.

One clear limitation of this model is that it has a bit of a strange relationship with time. A slightly pedantic issue is that the authors appear to be using rates and probabilities interchangeably. More importantly, enormous assumptions must be made in order to turn the cross-sectional data sources into what appears to be models over time. Issues in these assumptions and pre-model modelling can lead to severe misallocation of resources. It’s a very good point (not pedantic!) about rates vs probabilities - we have clarified this throughout. We have also added text in the limitations paragraph of the discussion section on the potential issues related to using single time-points as data sources for inform time-dependent estimates.

I believe this to be a useful tool, albeit one that would benefit greatly from real-world testing, and I hope that the authors are able to continue developing it. Thank you for taking the time to review!
I believe that this software appears to be a strong and useful effort toward making useful decisions based on cascades, under a generalized framework. The authors have identified an important problem, and have made substantial progress towards providing a useful solution. As a preliminary and experimental release, I believe this to be a successful effort. However, some caveats should be considered with regard to the software and its accompanying paper as they currently stand. We thank the reviewer for the summary.

A general concern is that software requires a high degree of sophistication and understanding of data and modelling to work as intended. The effort and sophistication required is highlighted in the example, where the assumptions required are often very serious, and highly consequential. This is well noted, and in response to this comment we have (a) revised the manuscript so it caters to a less technically knowledgeable audience, and (b) added text summarizing these concerns raised by the reviewer to the limitations paragraph of the discussion section.

In addition, the report as it stands could be more clearly organized and give additional technical detail in the methods section. We have attempted to streamline and clarify the methods section (also in response to comments from the other reviewers).

As the authors note, it shows promise and potential. Getting it from a proof of concept that solves very interesting problems to being useful/usable to relatively novice users is a long process. I really hope that this effort continues to develop into maturity. We thank the reviewer for the kind words and well wishes. As per a comment from the second reviewer, we have established a mechanism for gathering user feedback. We are looking forward to further improving our software in response to user comments.

Methods General comments: I would suggest a fairly substantial re-organization for this section. Quite a bit of time is spent on introducing people to the concept of a cascade (which is not the innovative part of this paper), at the expense of what is useful, interesting, and innovative about this tool. The section reads like a manual for designing a cascade analysis with the tool, rather than an explanation of what the software actually does and the methods and math underlying it. Quite a few sections are not the software methods at all, and should be moved to the introduction or removed. I am not sure I would be able to recreate a near equivalent of this tool without much more detail on the underlying model itself. I found that I did not understand how the model actually functioned, beyond that it was a compartmental model. Showing some of the math a bit more (even as an example, or just citations) would go a long way toward helping understand what's going on.We have rearranged this section significantly. Firstly, we have expanded the section on implementation (NB - the section headings are taken from the article guidelines on how software tool articles should be structured). The reviewer makes a good point that we were previously lacking detail on how the software is actually structured, so we have added this to the implementation section. Creating a similar tool would be possible by following the architecture in Figure 3. Much of the math behind the model is actually handled by the Atomica package, and we don’t go into detail about it here. However, we’ve added more detail in the example.

Designing the cascade: I think the language used for this framework could use a major revisit. It took me quite a bit of time and going backward to figure out what the authors were referring to throughout, which was distracting for the later sections. In the context of the user-oriented manual view, referring to the stages as "compartments" seems out of place and unnecessary, when "stage" or "state" seems more appropriate and more general for users. If this is an explanation of the methods of the model, then saying it is based on a compartmental model (and specifying exactly how said model is parameterized) is useful. "Parameter" has a much broader meaning, and forcing "parameter" to mean this very specific thing, is confusing. I would suggest referring to this as "transition properties" or "transition parameters" and collapse this paragraph with the previous. Also, what, specifically are the required parameters, and in what units? At minimum, transition rates need to be entered, correct? The same applies to the word "characteristics". Why not just use "stage groups" or similar? We have reworded this section (also noted in the comments from the two other reviewers). We wish to emphasize the connection between the cascade modelling methodology and compartmental models, so we have retained “compartment” and “transition”. We have also retained “parameter”, even though we agree it has a very broad meaning, because it is heavily entwined in the software itself and is used with internal consistency in this article. However, we have removed “characteristics” (also noted by another reviewer), and we have written a paragraph on the minimal data requirements. We intend for this section to help readers understand the relationship between a compartmental model and a cascade representation.

Collecting data: Again, a bit strange here. Data entry and data collection are two different things. Which are the authors trying to describe, and do they belong in the methods or in the use example? As an aside, I find the Excel interface bit difficult to use, and unintuitive why I would have to exit the site to enter data. It would be far more straightforward to have a browser-based UI for this, with optional support for Excel-based data entry. We renamed this section “Data entry”. We experimented with the idea of having users enter data via the web application itself, but experience with users led us to understand that people are very accustomed to entering data via Excel, and that doing so allows them to more easily share files with colleagues and collaborate effectively. In the end, we decided to offer Excel support since that’s what most users seemed to want.

Analysis of policy questions: I believe that this belongs in the intro. We have shifted this to the intro.

Cascade optimization: This is where the good stuff is! Lead with this, shorten/consolidate/remove the rest. I found this section to be relatively clear and well-written, but unfortunately buried underneath everything else. We have shortened the rest of the “Operation” section of the methods (again, this is a required section heading for this article type), so that this is placed more prominently in the methods.

Example cascade: One thing this section really highlights is the incredible amount of sophisticated work users need to do to make all this work together. Possibly to the point that a user who is able to adequately generate these numbers could very nearly model this all themselves. This is a first major effort, so that is to be expected, but it should be considered strongly. It would be helpful if this was more obviously linked to the compartments. Example: We estimated the transition rate from stage X to stage Y by ____. In our experience, it is not uncommon for people to have access to all the data summarized in this example section, but not to know how to combine it and analyze it to get policy recommendations.

"We further assume that the hypertension cascade is in a steady state such that the relative proportions of people in each cascade stage are constant over time, which implies that the number of people in each cascade stage will increase by 4.4% each year." This is a suspect and (as far as I can tell) unnecessary assumption. If this were true, there would be no change in the proportions between years (which there are, as shown in Figure 4). Why not use between-year flow rates (noting a few minor assumptions)? I might suggest that adding a mini model to solve for those flow rates would be an extremely useful feature, as forcing users to do this on their own will be error-prone. While is just an example, but it's a potentially distracting error. We have removed this.

Discussion: I would suggest that the discussion section have a much more comprehensive treatment of limitations of the tool. What kinds of things can it not model? Am I able to create a fully fledged SIR model, for example? That might be implied by the use of compartment modelling, it isn't clear to me whether or not this is possible. We have added a paragraph on limitations.

One clear limitation of this model is that it has a bit of a strange relationship with time. A slightly pedantic issue is that the authors appear to be using rates and probabilities interchangeably. More importantly, enormous assumptions must be made in order to turn the cross-sectional data sources into what appears to be models over time. Issues in these assumptions and pre-model modelling can lead to severe misallocation of resources. It’s a very good point (not pedantic!) about rates vs probabilities - we have clarified this throughout. We have also added text in the limitations paragraph of the discussion section on the potential issues related to using single time-points as data sources for inform time-dependent estimates.

I believe this to be a useful tool, albeit one that would benefit greatly from real-world testing, and I hope that the authors are able to continue developing it. Thank you for taking the time to review!
Competing Interests: No competing interests were disclosed. Close
Report a concern

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 07 Jun 2019

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2	3
Version 2 (revision) 24 Dec 19	read	read	read
Version 1 07 Jun 19	read	read	read

Noah Haber, University of North Carolina at Chapel Hill, Chapel Hill, USA; Stanford University, Stanford, USA
Ramnath Subbaraman, Tufts University School of Medicine, Boston, USA
Mathieu Maheu-Giroux, McGill University, Montréal, Canada

Comments on this article

All Comments(0)

Add a comment

Back to all reports

Reviewer Report

6 Views

16 Jan 2020 | for Version 2

Noah Haber, Carolina Population Center, University of North Carolina at Chapel Hill, Chapel Hill, NC, USA; Meta-Research Innovation Center, Stanford University, Stanford, CA, USA

6 Views Cite this report Responses(0)

Approved

I have re-read the document, and believe that the authors have greatly improved the paper all around. This is an excellent effort. I look forward to seeing future iterations of the concepts and software presented by this author team.

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

HIV, cascades, global health

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

4 Views

07 Jan 2020 | for Version 2

Ramnath Subbaraman, Department of Public Health and Community Medicine, Tufts University School of Medicine, Boston, MA, USA

4 Views Cite this report Responses(0)

Approved

The reviewers have addressed the primary feedback I provided, which was to provide feedback mechanism on the software platform they are describing. I approve the revised version of this manuscript.

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

tuberculosis implementation science, infectious diseases epidemiology

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

4 Views

06 Jan 2020 | for Version 2

Mathieu Maheu-Giroux, Department of Epidemiology, Biostatistics, and Occupational Health, McGill University, Montréal, QC, Canada

4 Views Cite this report Responses(0)

Approved

The authors have answered all my previous questions and concerns. I believe that the paper has been much improved.

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Population health; Infectious disease epidemiology; Mathematical modeling

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

12 Views

25 Jul 2019 | for Version 1

Mathieu Maheu-Giroux, Department of Epidemiology, Biostatistics, and Occupational Health, McGill University, Montréal, QC, Canada

12 Views Cite this report Responses(1)

Approved With Reservations

The authors could consider adding a table or box that would summarize the key data requirements to use this tool. I understand that this can be challenging given that the tool is intended to be generic but it would inform on the key elements required. For example, do we need mortality (or e0) and disease-specific mortality rates? Do we need to have precise estimates on the number (or %) of individuals in each compartment of the cascade?
In the case of infectious diseases where interventions can have externalities, how is onward transmission taken into account? From my understanding of the paper, there is no force of infection specified in the compartmental model. I am not saying that it should absolutely be considered but, at the very least, the assumption of no externalities (i.e., averting chains of transmission) should be made crystal clear in the paper and the implications on budget allocation discussed, including limitations.
It is unclear what are the types of outcomes that can be optimized? From the case studies on the website referred to in the paper (HIV in South Africa; https://cascade.tools/south-africa), it seems that it can be “infection averted” but this is not mentioned in the paper. Where the cascade results plugged in another model (e.g., Optima) to obtain this result?
Also, can QALY or DALY be optimized instead? Based on the sentence “It is possible for users to construct their own objective using any of the model’s outputs, as well as to combine multiple objectives into a single target”, this seems theoretically possible. In any case, I suggest being a little bit more specific about what type of objective functions can, and cannot, be optimized.
For resources allocation, what is the recommended time horizon for the economic evaluation/optimization? I suspect that this is case-specific and must be chosen by the users. I recommend making this clear in the paper. Similar issue with discounting? Can health outcomes and/or budgets be discounted at a user-specified rate? I am not asking that the authors go in details about this… but if these functionalities are readily available (or not) should be mentioned in the relevant section(s).
Also regarding resources allocation, can potential resources savings be considered? For example, earlier management of a chronic condition could save money down the line and this could impact decision-making regarding best allocative strategies.
The paper does an excellent job at explaining which type of questions can be answered with the Cascade Analysis Tool. It would be equally informative if examples of policy questions that cannot be answered (or with difficulty) were presented. For example, the optimization algorithm seems to be agnostic about equity constraints (is that the case)? Can resources allocation among cascades in different geographical regions be performed? Can optimizing two cascades (for different health conditions) that could share some common interventions be achieved?
Figure 5 is confusing as the “LTFU rate”, “Control rate”, and “Death rate” are depicted as unit-less probability. Are these rates (incidence density) or proportions (incidence proportion)?
Can the discussion of the limitations of the model be expanded. For example, what are the implications of the steady state assumption? How much training is needed for public health practitioners to be able to perform analyses on their own with the Cascade Analysis Tool? What set of minimum core competencies are required?

Discretionary revisions

The Methods section has many different types of headers without any clear ordering. Please standardize all headers and sub-headers as the current format is confusing.
Why start the methods with the different packages used (Implementation section)? I am not convinced that this is relevant to your audience.
“Characteristics” is confusing to described quantities that can be derived from the model? Maybe “Indicators” or “Derived metrics” would be more appropriate?
Is it really the “summed loss rates” that are being minimized or the total number of individuals lost at all stages? It seems that these two different ways of conceptualizing losses could give different results.
Why provide a link to the software page if it is password-protected? Will a fee be charged to use it?
Consider renaming the section “Use cases” to “Case studies”.
The GitHub repo refers to “Atomica”. It seems that the latter include more features than the Cascade Analysis Tool, which is slightly confusing. Also, the readme of this repo does not mention the Cascade Analysis Tool. Are “Atomica” and the “Cascade Analysis Tool” the same? If so, could the repo be renamed.

Is the rationale for developing the new software tool clearly explained?

Yes
Is the description of the software tool technically sound?

Yes
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Yes
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Partly
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Partly

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Population health; Infectious disease epidemiology; Mathematical modeling

Respond to this report

Responses (1)

Author Response

13 Jan 2020

Robyn Stuart, Department of Mathematical Sciences, University of Copenhagen, Universitetsparken 5, Copenhagen, 2100, Denmark

We thank the reviewer for taking the time to review, and for providing helpful comments that have greatly strengthened the article. Responses to particular points are provided below.

The paper by Kedziora and colleagues present a new software, christened “The Cascade Analysis Tool”, that enables users to optimize resources allocation under budget constraints. The authors provide a generic flexible framework to model different types of cascades, applicable to a wide range of health conditions. We thank the reviewer for the summary.
The introduction is well-written and provides a nice background to explain the relevance of the Cascade Analysis Tool. Overall, this is a nice paper that addresses an important issue. However, I found that the methods section is (at time) difficult to read and that some relevant information is missing. Thank you, we have reworked the methods section considerably in response to this and other reviewer comments - details are provided below.
The authors could consider adding a table or box that would summarize the key data requirements to use this tool. I understand that this can be challenging given that the tool is intended to be generic but it would inform on the key elements required. For example, do we need mortality (or e0) and disease-specific mortality rates? Do we need to have precise estimates on the number (or %) of individuals in each compartment of the cascade? We have added a summary paragraph on key data requirements to the methods section, as well as a link to the section of the website where this information is summarized.
In the case of infectious diseases where interventions can have externalities, how is onward transmission taken into account? From my understanding of the paper, there is no force of infection specified in the compartmental model. I am not saying that it should absolutely be considered but, at the very least, the assumption of no externalities (i.e., averting chains of transmission) should be made crystal clear in the paper and the implications on budget allocation discussed, including limitations. Atomica, the model that powers the Cascade Analysis Tool, can be used to set up arbitrary compartmental models, including models with a force of infection and onward transmission. This functionality is carried over to the Cascade Analysis Tool, but it’s not the main intended use case of the tool. We have tried to clarify this in the discussion section.
It is unclear what are the types of outcomes that can be optimized? From the case studies on the website referred to in the paper (HIV in South Africa; https://cascade.tools/south-africa), it seems that it can be “infection averted” but this is not mentioned in the paper. Where the cascade results plugged in another model (e.g., Optima) to obtain this result? We have added text to the limitations paragraph of the discussion section on this: “the web application was designed specifically for supporting cascade analyses, but the underlying model (Atomica) has additional functionalities that have not been introduced to the web application. For example, with Atomica one can specify a much broader range of optimization objectives (e.g. minimizing new infections, disease-related deaths, or DALYs), whereas the Cascade Analysis Tool web application only supports cascade-related objectives. Therefore, whilst it is possible to specify any compartmental model in the Cascade Analysis Tool (e.g. an SIR model with onward transmission), the set of analyses that can be conducted in the web application are limited to the cascade-related ones described in this paper.”
Also, can QALY or DALY be optimized instead? Based on the sentence “It is possible for users to construct their own objective using any of the model’s outputs, as well as to combine multiple objectives into a single target”, this seems theoretically possible. In any case, I suggest being a little bit more specific about what type of objective functions can, and cannot, be optimized. Yes, see above.
For resources allocation, what is the recommended time horizon for the economic evaluation/optimization? I suspect that this is case-specific and must be chosen by the users. I recommend making this clear in the paper. Similar issue with discounting? Can health outcomes and/or budgets be discounted at a user-specified rate? I am not asking that the authors go in details about this… but if these functionalities are readily available (or not) should be mentioned in the relevant section(s). Indeed, this is all to be specified by the user. Discounting is not currently supported, and we have added a note on this to the limitations section.
Also regarding resources allocation, can potential resources savings be considered? For example, earlier management of a chronic condition could save money down the line and this could impact decision-making regarding best allocative strategies. This is not possible, we’ve added this to the limitations.
The paper does an excellent job at explaining which type of questions can be answered with the Cascade Analysis Tool. It would be equally informative if examples of policy questions that cannot be answered (or with difficulty) were presented. For example, the optimization algorithm seems to be agnostic about equity constraints (is that the case)? Can resources allocation among cascades in different geographical regions be performed? Can optimizing two cascades (for different health conditions) that could share some common interventions be achieved? We’ve added some text addressing this point to the discussion section: “We are also working on extensions to the underlying model to support new types of policy questions, including questions around equity (e.g., which interventions should be prioritized to maximize equity of access to interventions like vaccines), geographical prioritization, and interrelated diseases (e.g., prioritization of integrated services for HIV/TB).”
Figure 5 is confusing as the “LTFU rate”, “Control rate”, and “Death rate” are depicted as unit-less probability. Are these rates (incidence density) or proportions (incidence proportion)? We have addressed this (also noted by reviewer 1).
Can the discussion of the limitations of the model be expanded. For example, what are the implications of the steady state assumption? How much training is needed for public health practitioners to be able to perform analyses on their own with the Cascade Analysis Tool? What set of minimum core competencies are required? We have significantly expanded the section on limitations and addressed these points.
The Methods section has many different types of headers without any clear ordering. Please standardize all headers and sub-headers as the current format is confusing.We have rearranged this section (also in response to comments from the other two reviewers). Why start the methods with the different packages used (Implementation section)? I am not convinced that this is relevant to your audience. According to the journal submission guidelines, this type of article needs to include subsections on Implementation (describing how the tool works and any relevant technical details required for implementation) and Operation (including the minimal system requirements needed to run the software and an overview of the workflow). This subsection on which packages were used was added as per an editor request.
“Characteristics” is confusing to described quantities that can be derived from the model? Maybe “Indicators” or “Derived metrics” would be more appropriate? We agree with this suggestion and have removed the word “characteristics”.
Is it really the “summed loss rates” that are being minimized or the total number of individuals lost at all stages? It seems that these two different ways of conceptualizing losses could give different results. We have changed to: “Minimize the total number of people lost from each stage of the cascade”.
Why provide a link to the software page if it is password-protected? Will a fee be charged to use it? The software requires users to log in, but it is free to create an account. New users can register by clicking “Register here” at http://ui.cascade.tools/
Consider renaming the section “Use cases” to “Case studies”.“Use cases” is suggested by the article submission guidelines.
The GitHub repo refers to “Atomica”. It seems that the latter include more features than the Cascade Analysis Tool, which is slightly confusing. Also, the readme of this repo does not mention the Cascade Analysis Tool. Are “Atomica” and the “Cascade Analysis Tool” the same? If so, could the repo be renamed. We agree it was confusing and have clarified in the text.

View more View less

Competing Interests

No competing interests were disclosed.

Back to all reports

Reviewer Report

14 Views

22 Jul 2019 | for Version 1

Ramnath Subbaraman, Department of Public Health and Community Medicine, Tufts University School of Medicine, Boston, MA, USA

14 Views Cite this report Responses(1)

Approved With Reservations

This is a very thoughtfully written article on a potentially helpful software tool. The goal of the tool is:

To facilitate the construction of care cascades for different diseases, including a flexible platform for developing such care cascades that recognizes that each disease will have different steps/stages required and different approaches to patient transitions between stages.
Facilitate construction of care cascade by specific sub-populations (e.g., gender, presumably age, etc.)
To allow estimation of the impact of interventions to improve outcomes in disease-specific care cascades.

Ideally, there would be some platform for public comment, critique, and feedback on this software platform as users engage with it. One of the challenges with reviewing this manuscript is that, while I spent a bit of time playing with the software, it is challenging to provide specific feedback on its strengths or deficiencies without actually using it in practice for a specific disease and programmatic analysis. As such, I think ongoing public feedback on the software from actual users is more critical than peer review of this manuscript.
Care cascades for different diseases deal with transitions differently. For example, most HIV care cascades look at transitions backwards as well as forwards across stages (or "compartments"). In contrast, in most care cascades for active TB, patients can only move forward across care cascade stages, and they can have multiple types of poor outcomes in each "gap" (i.e., difference between steps / stages / compartments). For example, for patients who start treatment but do not complete TB treatment, they could have one of 3 poor outcomes: (a) death, (b) treatment failure, and (c) loss to follow-up. The assumption is that "loss to follow-up" patients do not move "backwards" in the care cascade but fall out completely (and would have to restart from the beginning). Two questions related to this: (a) can this software modeling approach manage care cascades that only have transitions in the forward direction (I am assuming yes from Fig 3, but would be helpful to clarify); and (b) can this software modeling approach capture and estimate different types of poor outcomes as described above?

It would be helpful for the authors to add a few sentences explaining this point further. If we already have data on a particular intervention and its impact on reducing a given gap in care, what are the additional benefits of the type of modeling proposed by the authors?
One practical problem that users of this software will face may be the lack of available data on the effect sizes and costing of different interventions to reduce gaps in care. It would be helpful for the authors to specify what types of data / findings users of the software should have available to use this tool. Do they need effect sizes of an intervention to reduce a gap in the care cascade (i.e., estimated % reduction in a poor outcome at a particular step from an intervention)? Do they need confidence intervals for this effect estimate? Do they need these effect size estimates for an intervention for multiple care cascade steps (if an intervention improves outcomes at multiple steps)? What kind of costing data do they need to use this tool?

Authors might consider including a citation for the Lancet Global Health Commission on High-Quality Health Systems, as that major report has argued for care cascade analyses as being a central component of health quality dashboards for understanding quality of care. This strengthens the argument for a user friendly tool such as the one created by these authors.
In paragraph 2 of the paper, the authors should also note that the phrase "continuum of care" has also been used for these types of analyses. This is now emerging as the predominant language for these analyses in HIV, with the assumption that patients can move backwards as well as forwards along this continuum of care.
Paragraph 3 of the Introduction: The authors can correct the way they have described the TB care cascade analyses. The India and South Africa care cascades that have been cited for TB look at active TB disease, while the latent TB care cascade cited looks at latent TB disease. As such, these are two different frameworks for different types of TB--i.e., it is not that the framework in citation 10 guides the framework in citations 11 and 12--they are different frameworks for different forms of TB. A more detailed methods framework for active TB disease is available in the manuscript: Subbaraman R, Nathavitharana RR, Mayer KH, Satyanarayana S, Chadha VK, Arinaminpathy N, et al. (2019) Constructing care cascades for active tuberculosis: A strategy for program monitoring and identifying gaps in quality of care¹. Such methodological manuscripts could inform development of models using a tool such as the one the authors have created.

Is the rationale for developing the new software tool clearly explained?

Yes
Is the description of the software tool technically sound?

Yes
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Yes
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Yes
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Yes

References

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

tuberculosis implementation science, infectious diseases epidemiology

Respond to this report

Responses (1)

Author Response

13 Jan 2020

Robyn Stuart, Department of Mathematical Sciences, University of Copenhagen, Universitetsparken 5, Copenhagen, 2100, Denmark

Ideally, there would be some platform for public comment, critique, and feedback on this software platform as users engage with it. One of the challenges with reviewing this manuscript is that, while I spent a bit of time playing with the software, it is challenging to provide specific feedback on its strengths or deficiencies without actually using it in practice for a specific disease and programmatic analysis. As such, I think ongoing public feedback on the software from actual users is more critical than peer review of this manuscript. We thank the reviewer for this excellent suggestion. We have added a blog to our website (where we can also post information on updates to the tool). Users can provide feedback via the comments section.
Care cascades for different diseases deal with transitions differently. For example, most HIV care cascades look at transitions backwards as well as forwards across stages (or "compartments"). In contrast, in most care cascades for active TB, patients can only move forward across care cascade stages, and they can have multiple types of poor outcomes in each "gap" (i.e., difference between steps / stages / compartments). For example, for patients who start treatment but do not complete TB treatment, they could have one of 3 poor outcomes: (a) death, (b) treatment failure, and (c) loss to follow-up. The assumption is that "loss to follow-up" patients do not move "backwards" in the care cascade but fall out completely (and would have to restart from the beginning). Two questions related to this: (a) can this software modeling approach manage care cascades that only have transitions in the forward direction (I am assuming yes from Fig 3, but would be helpful to clarify); and (b) can this software modeling approach capture and estimate different types of poor outcomes as described above? Clarifying both of these questions in the text would be helpful for readers coming from different disease backgrounds and envisioning the approach differently. Yes, both types of cascade can be modelled with the tool. We have added text on this to the methods section.
A key point in the manuscript is this statement: "In many real-world situations, the impact of changing intervention coverage and the way interventions should be prioritized is not clear from the analysis of intervention properties alone." This is an important point that may not be evident to readers who don't frequently look at modeling data that look at broader implications and impacts of interventions. When I read this, I had a few thoughts regarding how the authors could expand on this point:
- It would be helpful for the authors to add a few sentences explaining this point further. If we already have data on a particular intervention and its impact on reducing a given gap in care, what are the additional benefits of the type of modeling proposed by the authors?
- One practical problem that users of this software will face may be the lack of available data on the effect sizes and costing of different interventions to reduce gaps in care. It would be helpful for the authors to specify what types of data / findings users of the software should have available to use this tool. Do they need effect sizes of an intervention to reduce a gap in the care cascade (i.e., estimated % reduction in a poor outcome at a particular step from an intervention)? Do they need confidence intervals for this effect estimate? Do they need these effect size estimates for an intervention for multiple care cascade steps (if an intervention improves outcomes at multiple steps)? What kind of costing data do they need to use this tool?
- Finally, it would be helpful for the authors to provide some real world examples of the types of studies that are available from which users of the software can provide these estimates. Even providing citations, example effect sizes or costing data from the existing literature for studies from HIV (for example, since they are most broadly available here) would help readers to think about the types of data they can seek out for their own diseases to populate these models.
We have:
- Moved this text to a more prominent position in the article, and emphasized it more clearly by repeating it in the discussion section as well.
- “One practical problem that users of this software will face may be the lack of available data on the effect sizes and costing of different interventions to reduce gaps in care.” -- we added a section noting the issues related to data availability in the methods.
- “It would be helpful for the authors to specify what types of data / findings users of the software should have available to use this tool.” - we added a section on minimum data requirements to the data entry section of the methods
- “Do they need effect sizes of an intervention to reduce a gap in the care cascade (i.e., estimated % reduction in a poor outcome at a particular step from an intervention)” -- yes, this is needed, and we’ve added text clarifying this.
- “Do they need confidence intervals for this effect estimate?” -- this is not required.
- “Do they need these effect size estimates for an intervention for multiple care cascade steps (if an intervention improves outcomes at multiple steps)? What kind of costing data do they need to use this tool?” - we have specified this in the data entry section.
- We have added a paragraph on typical data sources.
Authors might consider including a citation for the Lancet Global Health Commission on High-Quality Health Systems, as that major report has argued for care cascade analyses as being a central component of health quality dashboards for understanding quality of care. This strengthens the argument for a user friendly tool such as the one created by these authors. Thank you, we have added this.
In paragraph 2 of the paper, the authors should also note that the phrase "continuum of care" has also been used for these types of analyses. This is now emerging as the predominant language for these analyses in HIV, with the assumption that patients can move backwards as well as forwards along this continuum of care. Thank you, we have added this.
Paragraph 3 of the Introduction: The authors can correct the way they have described the TB care cascade analyses. The India and South Africa care cascades that have been cited for TB look at active TB disease, while the latent TB care cascade cited looks at latent TB disease. As such, these are two different frameworks for different types of TB--i.e., it is not that the framework in citation 10 guides the framework in citations 11 and 12--they are different frameworks for different forms of TB. A more detailed methods framework for active TB disease is available in the manuscript: Subbaraman R, Nathavitharana RR, Mayer KH, Satyanarayana S, Chadha VK, Arinaminpathy N, et al. (2019) Constructing care cascades for active tuberculosis: A strategy for program monitoring and identifying gaps in quality of care1. Such methodological manuscripts could inform development of models using a tool such as the one the authors have created. Thank you, we have fixed this and added the suggested citation.

View more View less

Competing Interests

No competing interests were disclosed.

Back to all reports

Reviewer Report

15 Views

25 Jun 2019 | for Version 1

Noah Haber, Carolina Population Center, University of North Carolina at Chapel Hill, Chapel Hill, NC, USA; Meta-Research Innovation Center, Stanford University, Stanford, CA, USA

15 Views Cite this report Responses(1)

Approved With Reservations

Is the rationale for developing the new software tool clearly explained?

Yes
Is the description of the software tool technically sound?

Yes
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Partly
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Yes
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Partly

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

HIV, cascades, global health

Respond to this report

Responses (1)

Author Response

13 Jan 2020

Robyn Stuart, Department of Mathematical Sciences, University of Copenhagen, Universitetsparken 5, Copenhagen, 2100, Denmark

I believe that this software appears to be a strong and useful effort toward making useful decisions based on cascades, under a generalized framework. The authors have identified an important problem, and have made substantial progress towards providing a useful solution. As a preliminary and experimental release, I believe this to be a successful effort. However, some caveats should be considered with regard to the software and its accompanying paper as they currently stand. We thank the reviewer for the summary.
A general concern is that software requires a high degree of sophistication and understanding of data and modelling to work as intended. The effort and sophistication required is highlighted in the example, where the assumptions required are often very serious, and highly consequential. This is well noted, and in response to this comment we have (a) revised the manuscript so it caters to a less technically knowledgeable audience, and (b) added text summarizing these concerns raised by the reviewer to the limitations paragraph of the discussion section.
In addition, the report as it stands could be more clearly organized and give additional technical detail in the methods section. We have attempted to streamline and clarify the methods section (also in response to comments from the other reviewers).
As the authors note, it shows promise and potential. Getting it from a proof of concept that solves very interesting problems to being useful/usable to relatively novice users is a long process. I really hope that this effort continues to develop into maturity. We thank the reviewer for the kind words and well wishes. As per a comment from the second reviewer, we have established a mechanism for gathering user feedback. We are looking forward to further improving our software in response to user comments.
Methods General comments: I would suggest a fairly substantial re-organization for this section. Quite a bit of time is spent on introducing people to the concept of a cascade (which is not the innovative part of this paper), at the expense of what is useful, interesting, and innovative about this tool. The section reads like a manual for designing a cascade analysis with the tool, rather than an explanation of what the software actually does and the methods and math underlying it. Quite a few sections are not the software methods at all, and should be moved to the introduction or removed. I am not sure I would be able to recreate a near equivalent of this tool without much more detail on the underlying model itself. I found that I did not understand how the model actually functioned, beyond that it was a compartmental model. Showing some of the math a bit more (even as an example, or just citations) would go a long way toward helping understand what's going on.We have rearranged this section significantly. Firstly, we have expanded the section on implementation (NB - the section headings are taken from the article guidelines on how software tool articles should be structured). The reviewer makes a good point that we were previously lacking detail on how the software is actually structured, so we have added this to the implementation section. Creating a similar tool would be possible by following the architecture in Figure 3. Much of the math behind the model is actually handled by the Atomica package, and we don’t go into detail about it here. However, we’ve added more detail in the example.
Designing the cascade: I think the language used for this framework could use a major revisit. It took me quite a bit of time and going backward to figure out what the authors were referring to throughout, which was distracting for the later sections. In the context of the user-oriented manual view, referring to the stages as "compartments" seems out of place and unnecessary, when "stage" or "state" seems more appropriate and more general for users. If this is an explanation of the methods of the model, then saying it is based on a compartmental model (and specifying exactly how said model is parameterized) is useful. "Parameter" has a much broader meaning, and forcing "parameter" to mean this very specific thing, is confusing. I would suggest referring to this as "transition properties" or "transition parameters" and collapse this paragraph with the previous. Also, what, specifically are the required parameters, and in what units? At minimum, transition rates need to be entered, correct? The same applies to the word "characteristics". Why not just use "stage groups" or similar? We have reworded this section (also noted in the comments from the two other reviewers). We wish to emphasize the connection between the cascade modelling methodology and compartmental models, so we have retained “compartment” and “transition”. We have also retained “parameter”, even though we agree it has a very broad meaning, because it is heavily entwined in the software itself and is used with internal consistency in this article. However, we have removed “characteristics” (also noted by another reviewer), and we have written a paragraph on the minimal data requirements. We intend for this section to help readers understand the relationship between a compartmental model and a cascade representation.
Collecting data: Again, a bit strange here. Data entry and data collection are two different things. Which are the authors trying to describe, and do they belong in the methods or in the use example? As an aside, I find the Excel interface bit difficult to use, and unintuitive why I would have to exit the site to enter data. It would be far more straightforward to have a browser-based UI for this, with optional support for Excel-based data entry. We renamed this section “Data entry”. We experimented with the idea of having users enter data via the web application itself, but experience with users led us to understand that people are very accustomed to entering data via Excel, and that doing so allows them to more easily share files with colleagues and collaborate effectively. In the end, we decided to offer Excel support since that’s what most users seemed to want.
Analysis of policy questions: I believe that this belongs in the intro. We have shifted this to the intro.
Cascade optimization: This is where the good stuff is! Lead with this, shorten/consolidate/remove the rest. I found this section to be relatively clear and well-written, but unfortunately buried underneath everything else. We have shortened the rest of the “Operation” section of the methods (again, this is a required section heading for this article type), so that this is placed more prominently in the methods.
Example cascade: One thing this section really highlights is the incredible amount of sophisticated work users need to do to make all this work together. Possibly to the point that a user who is able to adequately generate these numbers could very nearly model this all themselves. This is a first major effort, so that is to be expected, but it should be considered strongly. It would be helpful if this was more obviously linked to the compartments. Example: We estimated the transition rate from stage X to stage Y by ____. In our experience, it is not uncommon for people to have access to all the data summarized in this example section, but not to know how to combine it and analyze it to get policy recommendations.
"We further assume that the hypertension cascade is in a steady state such that the relative proportions of people in each cascade stage are constant over time, which implies that the number of people in each cascade stage will increase by 4.4% each year." This is a suspect and (as far as I can tell) unnecessary assumption. If this were true, there would be no change in the proportions between years (which there are, as shown in Figure 4). Why not use between-year flow rates (noting a few minor assumptions)? I might suggest that adding a mini model to solve for those flow rates would be an extremely useful feature, as forcing users to do this on their own will be error-prone. While is just an example, but it's a potentially distracting error. We have removed this.
Discussion: I would suggest that the discussion section have a much more comprehensive treatment of limitations of the tool. What kinds of things can it not model? Am I able to create a fully fledged SIR model, for example? That might be implied by the use of compartment modelling, it isn't clear to me whether or not this is possible. We have added a paragraph on limitations.
One clear limitation of this model is that it has a bit of a strange relationship with time. A slightly pedantic issue is that the authors appear to be using rates and probabilities interchangeably. More importantly, enormous assumptions must be made in order to turn the cross-sectional data sources into what appears to be models over time. Issues in these assumptions and pre-model modelling can lead to severe misallocation of resources. It’s a very good point (not pedantic!) about rates vs probabilities - we have clarified this throughout. We have also added text in the limitations paragraph of the discussion section on the potential issues related to using single time-points as data sources for inform time-dependent estimates.
I believe this to be a useful tool, albeit one that would benefit greatly from real-world testing, and I hope that the authors are able to continue developing it. Thank you for taking the time to review!

View more View less

Competing Interests

No competing interests were disclosed.

Alongside their report, reviewers assign a status to the article:

Approved - the paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations - A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approved - fundamental flaws in the paper seriously undermine the findings and conclusions

[1] 1. OECD: The Paris Declaration on Aid Effectiveness. 2005. Reference Source

[2] 2. OECD: The Accra Agenda For Action, 3rd High Level Forum on Aid Effectiveness. 2008. Reference Source

[3] 3. Biscaye P, LaFayette M, Martin A, et al.: Evaluating Donor-Level Results Measurement Systems. In EPAR Technical report. Evans School of Public Policy and Governance, 2015. Reference Source

[4] 4. Piot M: A Simulation model of case finding and treatment in tuberculosis control programmes. In WHO Global Tuberculosis Programme. World Health Organization: Geneva 1967. Reference Source

[5] 5. Gardner EM, McLees MP, Steiner JF, et al.: The spectrum of engagement in HIV care and its relevance to test-and-treat strategies for prevention of HIV infection. Clin Infect Dis. 2011; 52(6): 793–800. PubMed Abstract | Publisher Full Text | Free Full Text

[6] 6. Kilmarx PH, Mutasa-Apollo T: Patching a leaky pipe: the cascade of HIV care. Curr Opin HIV AIDS. 2013; 8(1): 59–64. PubMed Abstract

[7] 7. Gaolathe T, Wirth KE, Holme MP, et al.: Botswana's progress toward achieving the 2020 UNAIDS 90-90-90 antiretroviral therapy and virological suppression goals: a population-based survey. Lancet HIV. 2016; 3(5): e221–e230. PubMed Abstract | Publisher Full Text | Free Full Text

[8] 8. UNAIDS: Ending AIDS: progress towards the 90-90-90 targets. Geneva, 2017. Reference Source

[9] 9. Stop TB: Global Plan To End TB 2016-2020. 2015. Reference Source

[10] 10. Alsdurf H, Hill PC, Matteelli A, et al.: The cascade of care in diagnosis and treatment of latent tuberculosis infection: a systematic review and meta-analysis. Lancet Infect Dis. 2016; 16(11): 1269–1278. PubMed Abstract | Publisher Full Text

[11] 11. Naidoo P, Theron G, Rangaka MX, et al.: The South African Tuberculosis Care Cascade: Estimated Losses and Methodological Challenges. J Infect Dis. 2017; 216(suppl_7): S702–s713. PubMed Abstract | Publisher Full Text | Free Full Text

[12] 12. Subbaraman R, Nathavitharana RR, Satyanarayana S, et al.: The Tuberculosis Cascade of Care in India's Public Sector: A Systematic Review and Meta-analysis. PLoS Med. 2016; 13(10): e1002149. PubMed Abstract | Publisher Full Text | Free Full Text

[13] 13. Ali MK, Bullard KM, Gregg EW, et al.: A cascade of care for diabetes in the United States: visualizing the gaps. Ann Intern Med. 2014; 161(10): 681–689. PubMed Abstract | Publisher Full Text

[14] 14. Stokes A, Berry KM, Mchiza Z, et al.: Prevalence and unmet need for diabetes care across the care continuum in a national sample of South African adults: Evidence from the SANHANES-1, 2011-2012. PLoS One. 2017; 12(10): e0184264. PubMed Abstract | Publisher Full Text | Free Full Text

[15] 15. Linas BP, Barter DM, Leff JA, et al.: The hepatitis C cascade of care: identifying priorities to improve clinical outcomes. PLoS One. 2014; 9(5): e97317. PubMed Abstract | Publisher Full Text | Free Full Text

[16] 16. Murphy RD, Wohl AR, Ma Y, et al.: Adaptation of the HIV Care Continuum as a Method for Evaluating Syphilis and Gonorrhea Disease Control Activities in Los Angeles County. Sex Transm Dis. 2015; 42(12): 686–90. PubMed Abstract | Publisher Full Text

[17] 17. Perlman DC, Jordan AE, Nash D: Conceptualizing Care Continua: Lessons from HIV, Hepatitis C Virus, Tuberculosis and Implications for the Development of Improved Care and Prevention Continua. Front Public Health. 2017; 4: 296. PubMed Abstract | Publisher Full Text | Free Full Text

[18] 18. Socias ME, Volkow N, Wood E: Adopting the 'cascade of care' framework: an opportunity to close the implementation gap in addiction care? Addiction. 2016; 111(12): 2079–2081. PubMed Abstract | Publisher Full Text | Free Full Text

[19] 19. Williams AR, Nunes E, Olfson M: To Battle The Opioid Overdose Epidemic, Deploy The ‘Cascade Of Care’ Model. In Health Affairs Blog. 2017. Reference Source

[20] 20. Lessard L, Fournier L, Gauthier J, et al.: Continuum of care for persons with common mental health disorders in Nunavik: a descriptive study. Int J Circumpolar Health. 2015; 74(1): 27186. PubMed Abstract | Publisher Full Text | Free Full Text

[21] 21. Olney JJ, Braitstein P, Eaton JW, et al.: Evaluating strategies to improve HIV care outcomes in Kenya: a modelling study. Lancet HIV. 2016; 3(12): e592–e600. PubMed Abstract | Publisher Full Text | Free Full Text

[22] 22. Price AJ, Crampin AC, Amberbir A, et al.: Prevalence of obesity, hypertension, and diabetes, and cascade of care in sub-Saharan Africa: a cross-sectional, population-based study in rural and urban Malawi. Lancet Diabetes Endocrinol. 2018; 6(3): 208–222. PubMed Abstract | Publisher Full Text | Free Full Text

[23] 23. Hajjar I, Kotchen JM, Kotchen TA: Hypertension: trends in prevalence, incidence, and control. Annu Rev Public Health. 2006; 27(1): 465–490. PubMed Abstract | Publisher Full Text

[24] 24. Diez Roux AV, Chambless L, Merkin SS, et al.: Socioeconomic disadvantage and change in blood pressure associated with aging. Circulation. 2002; 106(6): 703–710. PubMed Abstract | Publisher Full Text

[25] 25. Ford ES: Trends in mortality from all causes and cardiovascular disease among hypertensive and nonhypertensive adults in the United States. Circulation. 2011; 123(16): 1737–1744. PubMed Abstract | Publisher Full Text

[26] 26. McGillen JB, Anderson SJ, Dybul MR, et al.: Optimum resource allocation to reduce HIV incidence across sub-Saharan Africa: a mathematical modelling study. Lancet HIV. 2016; 3(9): e441–8. PubMed Abstract | Publisher Full Text

[27] 27. Atomica Team: atomicateam/atomica v1.4.0 (Version v1.4.0). Zenodo. 2019. http://www.doi.org/10.5281/zenodo.3137154

The Cascade Analysis Tool: software to analyze and optimize care cascades

Abstract

Keywords

Introduction

Figure 1. A typical cascade presents the proportion of the total target population that have attained each of the sequential steps of engagement in the path towards a successful outcome.

Figure 2. The types of questions designed to be answered by the Cascade Analysis Tool.

Methods

Implementation

Operation

Figure 3. A generic treatment cascade (panel A), which is translated (panel B) into a compartmental model (panel C).

Use cases

Designing the cascade

Collating data

Figure 5. Illustration of the data entry book for the hypertension example depicted in Figure 4.

Table 1. Illustrative data on interventions for the hypertension example presented in Figure 4.

Analysis of policy questions

Table 2. Illustrative scenarios showing different intervention scale-up options, based on the treatment cascade introduced in Figure 3.

Figure 6. The state of the illustrative hypertension cascade in 2017 under the 6 different scale-up options presented in Table 2.

Figure 7. Optimal allocations for achieving difference targets related to the illustrative hypertension example.

Discussion

Data availability

Software availability

Grant information

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Are you a Gates-funded researcher?

Thank you!

The Cascade Analysis Tool: software to analyze and optimize care cascades

Abstract

Keywords

Introduction

Figure 1. A typical cascade presents the proportion of the total target population that have attained each of the sequential steps of engagement in the path towards a successful outcome.

Figure 2. The types of questions designed to be answered by the Cascade Analysis Tool.

Methods

Implementation

Operation

Figure 3. A generic treatment cascade (panel A), which is translated (panel B) into a compartmental model (panel C).

Use cases

Designing the cascade

Collating data

Figure 5. Illustration of the data entry book for the hypertension example depicted in Figure 4.

Table 1. Illustrative data on interventions for the hypertension example presented in Figure 4.

Analysis of policy questions

Table 2. Illustrative scenarios showing different intervention scale-up options, based on the treatment cascade introduced in Figure 3.

Figure 6. The state of the illustrative hypertension cascade in 2017 under the 6 different scale-up options presented in Table 2.

Figure 7. Optimal allocations for achieving difference targets related to the illustrative hypertension example.

Discussion

Data availability

Software availability

Grant information

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Competing Interests Policy

Stay Updated

Are you a Gates-funded researcher?

Thank you!